题目内容
若m<n,比较下列各式的大小:
(1)m-3______n-3 (2)-5m______-5n (3)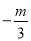 ______
______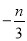
(4)3-m______2-n (5)0_____m-n (6)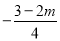 _____
_____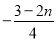
 < > > > > <
【解析】(1)m
< > > > > <
【解析】(1)m
练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
用计算器求下列格式的值(结果精确到0.0001).
(1)tan63°27′;
(2)cos18°59′27″;
(3)sin67°38′24″.
 (1)2.0013;(2)0.9456;(3)0.9248.
【解析】试题分析:将度、分、秒统一为度,然后利用计算器即可求出结果.
试题解析:
【解析】
(1)tan63°27′=tan63.45°≈2.0013;
(2)cos18°59′27″=cos18.9908°≈0.9456;
(3)sin67°38′24″=sin67.64°≈0.9248.
(1)2.0013;(2)0.9456;(3)0.9248.
【解析】试题分析:将度、分、秒统一为度,然后利用计算器即可求出结果.
试题解析:
【解析】
(1)tan63°27′=tan63.45°≈2.0013;
(2)cos18°59′27″=cos18.9908°≈0.9456;
(3)sin67°38′24″=sin67.64°≈0.9248. 一个不透明的袋中共有20个球,它们除颜色不同外,其余均相同,其中8个白球,5个黄球,5个绿球,2个红球,则任意摸出一个球是红球的概率是( )
A.  B.
B. 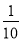 C.
C. 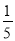 D.
D. 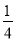
 B
【解析】【解析】
∵20个球中红球有2个,∴任意摸出一个球是红球的概率是=,故选B.
B
【解析】【解析】
∵20个球中红球有2个,∴任意摸出一个球是红球的概率是=,故选B. 下列数值中,是不等式x-2>2的一个解的是( )
A. 0 B. 2
C. 4 D. 6
 D
【解析】解不等式x?2>2,得x>4,
而大于4的数只有6.
故选D.
D
【解析】解不等式x?2>2,得x>4,
而大于4的数只有6.
故选D. 若ax>b,ac2<0,则x________.
 <
【解析】由ac2<0,结合c2为正可知a<0,
对ax>b两边同时除以a,得x< .故答案为:<.
<
【解析】由ac2<0,结合c2为正可知a<0,
对ax>b两边同时除以a,得x< .故答案为:<. 如果t>0,那么a+t与a的大小关系是( )
A、a+t>a B、a+t<a C、a+t≥a D、不能确定
 A
【解析】
试题分析:根据不等式的基本性质即可得到结果.
t>0,
∴a+t>a,
故选A.
A
【解析】
试题分析:根据不等式的基本性质即可得到结果.
t>0,
∴a+t>a,
故选A. 在△ABC中,AB=13cm,AC=20cm,BC边上的高为12cm,则△ABC的面积为________cm2.
 126或66
【解析】试题分析:此题分两种情况:∠B为锐角或∠B为钝角已知AB、AC的值,利用勾股定理即可求出BC的长,利用三角形的面积公式得结果.
【解析】
当∠B为锐角时(如图1),
在Rt△ABD中,
BD===5cm,
在Rt△ADC中,
CD===16cm,
∴BC=21,
∴S△ABC==×21×12=126cm2;
当∠B为钝角...
126或66
【解析】试题分析:此题分两种情况:∠B为锐角或∠B为钝角已知AB、AC的值,利用勾股定理即可求出BC的长,利用三角形的面积公式得结果.
【解析】
当∠B为锐角时(如图1),
在Rt△ABD中,
BD===5cm,
在Rt△ADC中,
CD===16cm,
∴BC=21,
∴S△ABC==×21×12=126cm2;
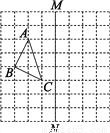
当∠B为钝角... 如图,在正方形网格上有一个△ABC.
(1)作△ABC关于直线MN的对称图形(不写作法);
(2)在网格上的最小正方形的边长为1,求△ABC的面积.
 (1)见解析;(2)
【解析】试题分析:(1)根据网格特点分别找到A、B、C关于直线MN对称的点,然后顺次连接即可得;
(2)用三角形ABC所在长方形的面积减去四周三个小三角形的面积即可得.
试题解析:(1)如图所示:
(2)S△ABC=2×3-2×(×1×2)-×1×3=.
(1)见解析;(2)
【解析】试题分析:(1)根据网格特点分别找到A、B、C关于直线MN对称的点,然后顺次连接即可得;
(2)用三角形ABC所在长方形的面积减去四周三个小三角形的面积即可得.
试题解析:(1)如图所示:
(2)S△ABC=2×3-2×(×1×2)-×1×3=. 关于x的方程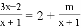 无解,则m的值为( )
无解,则m的值为( )
A. ﹣5 B. ﹣8 C. ﹣2 D. 5
 A
【解析】试题分析:去分母得:3x﹣2=2x+2+m,由分式方程无解,得到x+1=0,即x=﹣1,代入整式方程得:﹣5=﹣2+2+m,解得:m=﹣5,故选A.
A
【解析】试题分析:去分母得:3x﹣2=2x+2+m,由分式方程无解,得到x+1=0,即x=﹣1,代入整式方程得:﹣5=﹣2+2+m,解得:m=﹣5,故选A. 
