如图,△ABC中,∠A=60°,∠ABC、∠ACB的平分线BD、CD交于点D,则∠BDC=_____.
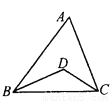
 120°
【解析】试题解析:在△ABC中,
∵BD是∠ABC的平分线,CD是∠ACB的平分线,
在△BCI中,
故答案为:
120°
【解析】试题解析:在△ABC中,
∵BD是∠ABC的平分线,CD是∠ACB的平分线,
在△BCI中,
故答案为: 如图,该五角星中,∠A+∠B+∠C+∠D+∠E=________度.
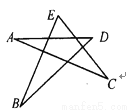
 180°
【解析】试题解析:如图所示:
∵∠DGE是△EGB的外角,∴∠DGF=∠B+∠E,
∵∠DFG是△AFC的外角,∴∠DFG=∠A+∠C,
∵∠DFG+∠DGF+∠D=
∴∠A+∠B+∠C+∠D+∠E=
故答案是:180.
180°
【解析】试题解析:如图所示:
∵∠DGE是△EGB的外角,∴∠DGF=∠B+∠E,
∵∠DFG是△AFC的外角,∴∠DFG=∠A+∠C,
∵∠DFG+∠DGF+∠D=
∴∠A+∠B+∠C+∠D+∠E=
故答案是:180. 如图,点B、C、D、E共线,试问图中A、B、C、D、E五点可确定多少个三角形?说明理由.
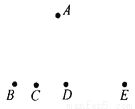
 6个.
【解析】试题分析:经过两点可以确定一条线段,而不在同一条直线上的三条线段首尾顺次相接可组成一个三角形,因而三角形的个数就是B、C、D、E四点中,两个分成一组,点的组数.
试题解析:可以确定6个三角形.
理由:经过两点可以确定一条线段,而不在同一条直线上的三条线段首尾顺次相接可组成一个三角形,
所以图中可以确定6个三角形.
6个.
【解析】试题分析:经过两点可以确定一条线段,而不在同一条直线上的三条线段首尾顺次相接可组成一个三角形,因而三角形的个数就是B、C、D、E四点中,两个分成一组,点的组数.
试题解析:可以确定6个三角形.
理由:经过两点可以确定一条线段,而不在同一条直线上的三条线段首尾顺次相接可组成一个三角形,
所以图中可以确定6个三角形. 如图,∠BAD=∠CAD,则AD是△ABC的角平分线,对吗?说明理由.
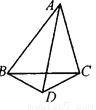
 不是,理由见解析.
【解析】试题分析:考查了三角形的角平分线的定义,三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线.
试题解析:根据三角形的角平分线的定义,可知:①平分三角形的一个内角;②是一条线段,一个端点是三角形的顶点,另一点在这个顶点的对边上.而此题中AD满足①,但点D不在BC边上,故不满足②.所以,AD不是△ABC的角平分...
不是,理由见解析.
【解析】试题分析:考查了三角形的角平分线的定义,三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线.
试题解析:根据三角形的角平分线的定义,可知:①平分三角形的一个内角;②是一条线段,一个端点是三角形的顶点,另一点在这个顶点的对边上.而此题中AD满足①,但点D不在BC边上,故不满足②.所以,AD不是△ABC的角平分... 一个飞机零件的形状如图5—19所示,按规定∠A应等于90°,∠B,∠D应分别是20°和30°,康师傅量得∠BCD=143°,就能断定这个零件不合格,你能说出其中的道理吗?
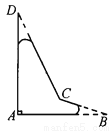
 不合格,理由见解析.
【解析】试题分析:延长BC与AD相交于点E,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BCD即可判断.
试题解析:如图,延长BC与AD相交于点E,
∵∠1是△ABE的外角,
同理,
∵李师傅量得不是
∴这个零件不合格.
不合格,理由见解析.
【解析】试题分析:延长BC与AD相交于点E,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BCD即可判断.
试题解析:如图,延长BC与AD相交于点E,
∵∠1是△ABE的外角,
同理,
∵李师傅量得不是
∴这个零件不合格. 如图,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多5cm,AB与AC的和为11cm,求AC的长.
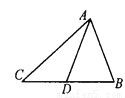
 8cm.
【解析】试题分析:根据中线的定义知CD=BD,结合三角形的周长公式知AC﹣AB=5cm,又AB+AC=11cm,易求AC的长度.
试题解析:∵AD是BC边上的中线,
∴D为BC的中点,CD=BD.
∵△ADC的周长﹣△ABD的周长=5cm.
∴AC﹣AB=5cm.
又∵AB+AC=11cm,
∴AC=8cm.即AC的长度是8cm.
8cm.
【解析】试题分析:根据中线的定义知CD=BD,结合三角形的周长公式知AC﹣AB=5cm,又AB+AC=11cm,易求AC的长度.
试题解析:∵AD是BC边上的中线,
∴D为BC的中点,CD=BD.
∵△ADC的周长﹣△ABD的周长=5cm.
∴AC﹣AB=5cm.
又∵AB+AC=11cm,
∴AC=8cm.即AC的长度是8cm. 如图,△ABC中,∠B=34°,∠ACB=104°,AD是BC边上的高,AE是∠BAC的平分线,求∠DAE的度数.
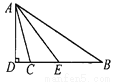
 35°.
【解析】由三角形的内角和定理,可求∠BAC=70°,又由AE是∠BAC的平分线,可求∠BAE=35°,再由AD是BC边上的高,可知∠ADB=90°,可求∠BAD=25°,所以∠DAE=∠BAE-∠BAD=10°.
【解析】
在△ABC中,
∵∠BAC=180°-∠B-∠C=70°,
∵AE是∠BAC的平分线,
∴∠BAE=∠CAE=35°.
又∵AD是BC边上的高,...
35°.
【解析】由三角形的内角和定理,可求∠BAC=70°,又由AE是∠BAC的平分线,可求∠BAE=35°,再由AD是BC边上的高,可知∠ADB=90°,可求∠BAD=25°,所以∠DAE=∠BAE-∠BAD=10°.
【解析】
在△ABC中,
∵∠BAC=180°-∠B-∠C=70°,
∵AE是∠BAC的平分线,
∴∠BAE=∠CAE=35°.
又∵AD是BC边上的高,... 如图,在△ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm,求:(1)△ABC的面积;(2)CD的长.
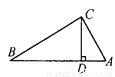
 (1)30cm2;(2) cm.
【解析】(1)根据直角三角形面积的求法,即可得出△ABC的面积,
(2)根据三角形的面积公式即可求得CD的长,
【解析】
(1)∵∠ACB=90°,BC=12cm,AC=5cm,
∴S△ABC=BC×AC=30cm2,
(2)∵S△ABC=AB×CD=30cm2,
∴CD=30÷AB=cm,
(1)30cm2;(2) cm.
【解析】(1)根据直角三角形面积的求法,即可得出△ABC的面积,
(2)根据三角形的面积公式即可求得CD的长,
【解析】
(1)∵∠ACB=90°,BC=12cm,AC=5cm,
∴S△ABC=BC×AC=30cm2,
(2)∵S△ABC=AB×CD=30cm2,
∴CD=30÷AB=cm, 已知:如图,P是△ABC内任一点,求证:∠BPC>∠A.
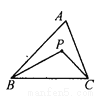
 说明见解析.
【解析】试题分析:延长BP交AC于D. 根据△PDC外角的性质知∠BPC>∠PDC,根据△ABD外角的性质知∠PDC>∠A,所以易证∠BPC>∠A.
试题解析:如图,延长BP交AC于D.
∵∠BPC>∠PDC,∠PDC>∠A,
∴∠BPC>∠A.
说明见解析.
【解析】试题分析:延长BP交AC于D. 根据△PDC外角的性质知∠BPC>∠PDC,根据△ABD外角的性质知∠PDC>∠A,所以易证∠BPC>∠A.
试题解析:如图,延长BP交AC于D.
∵∠BPC>∠PDC,∠PDC>∠A,
∴∠BPC>∠A.