题目内容
如图，点B、C、D、E共线，试问图中A、B、C、D、E五点可确定多少个三角形?说明理由．
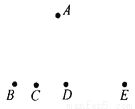
6个.
【解析】试题分析：经过两点可以确定一条线段，而不在同一条直线上的三条线段首尾顺次相接可组成一个三角形，因而三角形的个数就是B、C、D、E四点中，两个分成一组，点的组数．
试题解析：可以确定6个三角形.
理由：经过两点可以确定一条线段，而不在同一条直线上的三条线段首尾顺次相接可组成一个三角形，
所以图中可以确定6个三角形.
练习册系列答案
相关题目
如果直线a∥b，b∥c，那么a∥c。这个推理的依据是（ ）
A. 等量代换； B. 平行公理；
C. 两直线平行，同位角相等； D. 平行于同一直线的两条直线平行。
D
【解析】试题分析：在同一平面内，平行于同一条直线的两直线平行，故本题选D． 在△ABC中，∠C＝90°，a＝5，c＝17，用科学计算器求∠A约等于 ( )
A. 17.6° B. 17°6′ C. 17°16′ D. 17.16°
A
【解析】试题解析：sinA=，
A=sin-10.294=17.6°，
故选A． 将点A(3，2)沿x轴向左平移4个单位长度得到点A′，则点A′关于原点对称的点的坐标是( )
A. (-3，2) B. (-1，2) C. (1，2) D. (1，-2)
D
【解析】试题分析：将点A（3，2）向左平移4个单位长度得点A′，可得点A′的坐标为（﹣1，2），所以点A′关于y轴对称的点的坐标是（1，2），故选D． 如图，在△ABC中，∠ACB=90°，CD是AB边上的高，AB=13cm，BC=12cm，AC=5cm，求：(1)△ABC的面积；(2)CD的长．
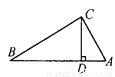
(1)30cm2;(2) cm.
【解析】（1）根据直角三角形面积的求法，即可得出△ABC的面积，
（2）根据三角形的面积公式即可求得CD的长，
【解析】
（1）∵∠ACB=90°，BC=12cm，AC=5cm，
∴S△ABC=BC×AC=30cm2，
（2）∵S△ABC=AB×CD=30cm2，
∴CD=30÷AB=cm， 如图5—13，在△ABC中，AD⊥BC，GC⊥BC，CF⊥AB，BE⊥AC，垂足分别为D、C、F、E，则_______是△ABC中BC边上的高，_________是△ABC中AB边上的高，_________是 △ABC中AC边上的高，CF是△ABC的高，也是△_______、△_______、△_______、△_________的高．
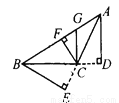
AD CF BE BFC FGC FAC GAC
【解析】试题解析：AD是△ABC中BC边上的高，是△ABC中AB边上的高，BE是△ABC中AC边上的高，CF是△ABC的高，也是△BFC、△FGC、△FAC、△GAC的高.
故答案是：AD、CF、BE、BFC、FGC、FAC、GAC. 五条线段的长分别为1，2，3，4，5，以其中任意三条线段为边长可以________个三角形．
3
【解析】试题解析：由三角形的两边之和大于第三边,两边之差小于第三边可知
在所给数组中能组成三角形的是2、3、4;2、4、5和3、4、5三组.
故答案为：3. (1)请指出小明的作业(如图)从哪一步开始出现错误，更正过来，并计算出正确结果；
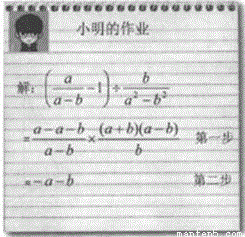
(2)若a，b是不等式组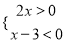
的整数解(a＜b)，求(1)中分式的值．
（1）小明第一步中括号内计算错了，a＋b；（2）3
【解析】试题分析：（1）根据题意，先算括号里面的（通分后进行相减），且把除法转化为乘法，然后约分即可判断错误点，并改错；
（2）通过解不等式组，求出x的取值范围，然后取分母不为0的之代入可求值.
试题解析：(1)小明第一步中括号内计算错了；
原式＝×＝ ×＝a＋b.
(2)∵解不等式2x>0得x＞0，解不等式x－3<... 在Rt△ABC中，∠C=90°，CD是斜边AB上的高，如果CD=3，BD=2．求cos∠A的值.
【解析】分析：根据题意画出图形，进而利用锐角三角函数关系得出cosA=cos∠BCD进而求出即可．
本题解析：
如图所示：
∵∠ACB=90°，∴∠B+∠A=90°，
∵CD⊥AB，∴∠CDA=90°，∴∠B+∠BCD=90°，∴∠BCD=∠A，
∵CD=3，BD=2，∴BC=
∴cosA=cos∠BCD=
故答案为：