练习册系列答案
相关题目
如图，如果AB∥CD，CD∥EF，那么∠BCE等于（ ）
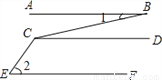
A. ∠1＋∠2 B. ∠2－∠1 C. 180°－∠2＋∠1 D. 180°－∠1＋∠2
C
【解析】试题分析：根据AB∥CD可得：∠BCD=∠1；根据CD∥EF可得：∠2+∠DCE=180°，则∠DCE=180°-∠2，则∠BCE=∠BCD+∠DCE=∠1+180°-∠2，故选C． 在△ABC中，∠C＝90°，a＝5，c＝17，用科学计算器求∠A约等于 ( )
A. 17.6° B. 17°6′ C. 17°16′ D. 17.16°
A
【解析】试题解析：sinA=，
A=sin-10.294=17.6°，
故选A． 设点A与点B关于x轴对称，点A与点C关于y轴对称，则点B与点C( )
A. 关于x轴对称 B. 关于y轴对称 C. 关于原点对称． D. 既关于x轴对称，又关于y轴对称
C
【解析】根据关于x轴对称的点的坐标规律:横坐标相同,纵坐标互为相反数,关于原点的对称点,横纵坐标都变成相反数,关于y轴对称的点的坐标规律:横坐标互为相反数,纵坐标相同,
点A与点B关于x轴对称,点A与点C关于y轴对称,则点B与点C原点对称,故选C. 如图，△ABC中，∠B=34°，∠ACB=104°，AD是BC边上的高，AE是∠BAC的平分线，求∠DAE的度数．
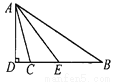
35°.
【解析】由三角形的内角和定理，可求∠BAC=70°，又由AE是∠BAC的平分线，可求∠BAE=35°，再由AD是BC边上的高，可知∠ADB=90°，可求∠BAD=25°，所以∠DAE=∠BAE-∠BAD=10°．
【解析】
在△ABC中，
∵∠BAC=180°-∠B-∠C=70°，
∵AE是∠BAC的平分线，
∴∠BAE=∠CAE=35°．
又∵AD是BC边上的高，... 在△ABC中，∠A－∠B=30°、∠C=4∠B，则∠C=________．
100°
【解析】试题解析：
①，
②，
①?②得, 解得
故答案为： 各边长均为整数且三边各不相等的三角形的周长小于13，这样的三角形个数共有( )
A. 5个 B. 4个 C. 3个 D. 2个
C
【解析】试题解析：根据三角形的两边之和大于第三边以及三角形的周长小于13，则其中的任何一边不能超过6.5；
再根据两边之差小于第三边，则这样的三角形共有3，4，2；4，5，2；3，4，5三个.
故选C. 某商场购进甲、乙两种商品，乙商品的单价是甲商品单价的2倍，若设甲商品的单价为x元，则购买240元甲商品的数量比购买300元乙商品的数量多____件．
【解析】设甲商品的单价为x元，乙商品的单价为2x元，根据购买240元甲商品的数量比购买300元乙商品的数量多．
故答案为： . 如图，在Rt△ABC中，∠C＝90°，AB＝2BC，则sinB的值为 .
【解析】试题分析：因为在Rt△ABC中，∠C = 90°，AB = 2BC，所以．