��Ŀ����
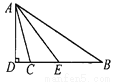
��ͼ����ABC�У���B=34�㣬��ACB=104�㣬AD��BC���ϵĸߣ�AE�ǡ�BAC��ƽ���ߣ����DAE�Ķ�����
 35��.
���������������ε��ڽǺͶ����������BAC=70�㣬����AE�ǡ�BAC��ƽ���ߣ������BAE=35�㣬����AD��BC���ϵĸߣ���֪��ADB=90�㣬�����BAD=25�㣬���ԡ�DAE=��BAE-��BAD=10�㣮
��������
�ڡ�ABC�У�
�ߡ�BAC=180��-��B-��C=70�㣬
��AE�ǡ�BAC��ƽ���ߣ�
���BAE=��CAE=35�㣮
�֡�AD��BC���ϵĸߣ�...
35��.
���������������ε��ڽǺͶ����������BAC=70�㣬����AE�ǡ�BAC��ƽ���ߣ������BAE=35�㣬����AD��BC���ϵĸߣ���֪��ADB=90�㣬�����BAD=25�㣬���ԡ�DAE=��BAE-��BAD=10�㣮
��������
�ڡ�ABC�У�
�ߡ�BAC=180��-��B-��C=70�㣬
��AE�ǡ�BAC��ƽ���ߣ�
���BAE=��CAE=35�㣮
�֡�AD��BC���ϵĸߣ�...
��ϰ��ϵ�д�
�����Ŀ
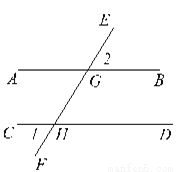
��֪����ͼ��ֱ��EF��AB��CD�ֱ��ཻ�ڵ�G��H����1=��3��
��֤��AB��CD��
 ֤��������
��������������������ȸ��ݶԶ��ǵ����ʵó���AGH=��GHD���������ڴ��������ֱ��ƽ�еó��𰸣�
����������ߡ�1=��GHD����3=��AGH���Զ�����ȣ�����1=��3����֪�������AGH=��GHD��
��AB��CD���ڴ�����ȣ��ڴ�����ȣ���
֤��������
��������������������ȸ��ݶԶ��ǵ����ʵó���AGH=��GHD���������ڴ��������ֱ��ƽ�еó��𰸣�
����������ߡ�1=��GHD����3=��AGH���Զ�����ȣ�����1=��3����֪�������AGH=��GHD��
��AB��CD���ڴ�����ȣ��ڴ�����ȣ��� 2013��4��20���Ű�«ɽ�ط���7.0������ij��Ԯ�Ӹϸ������μӾ�Ԯ����Ԯ��Ա����һ��Ϊ20m�����ӣ�Ϊ��ȫ������ӿ���ǽ�ϵĸ߶Ȳ��ܳ���17.3m.�����������ļнDz�����___��ʱ���ǰ�ȫ�ģ�(��ȷ��1��)
 59
����������������������ӿ�ס��ǽ�ϵĸ߶Ȳ��ܳ���17.3m��
�����������ļн����Ϊ
���A���Ϊ
�ʴ�Ϊ��
59
����������������������ӿ�ס��ǽ�ϵĸ߶Ȳ��ܳ���17.3m��
�����������ļн����Ϊ
���A���Ϊ
�ʴ�Ϊ�� ��֪��M������Ϊ(3��-5)�������x��ԳƵĵ�������M��������Ϊ___________������y��ԳƵĵ�M��������Ϊ___________������ԭ��ԳƵĵ������Ϊ____________.
 (3��5) (-3��-5) (-3��5)
�����������ݹ���x��ԳƵĵ���������:��������ͬ,�����껥Ϊ�෴��,����ԭ��ĶԳƵ�,�������궼����෴��,����y��ԳƵĵ���������:�����껥Ϊ�෴��,��������ͬ,���Ե�M��3, ��5������x��ԳƵĵ������Ϊ��3, 5��,����y��ԳƵ������Ϊ��-3,-5��,����ԭ��ԳƵĵ������Ϊ��-3,5��,�ʴ�Ϊ: ��3, 5��, ��-3,-5��, ��...
(3��5) (-3��-5) (-3��5)
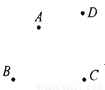
�����������ݹ���x��ԳƵĵ���������:��������ͬ,�����껥Ϊ�෴��,����ԭ��ĶԳƵ�,�������궼����෴��,����y��ԳƵĵ���������:�����껥Ϊ�෴��,��������ͬ,���Ե�M��3, ��5������x��ԳƵĵ������Ϊ��3, 5��,����y��ԳƵ������Ϊ��-3,-5��,����ԭ��ԳƵĵ������Ϊ��-3,5��,�ʴ�Ϊ: ��3, 5��, ��-3,-5��, ��... ��ͼ��ԥ�����ĸ���ׯA��B��C��D������Ҫ����һ��ˮ��P����ش�ˮ��PӦ���ں�λ�ã�����ʹ����4��ľ���֮����С��˵�����Լ���ϵİ취�����ɣ�
 ˵��������.
����������������������߶ε����ʣ�����֮�䣬�߶ξ�����̣�������⣬Ҫʹ�����ĸ���ׯ�ľ���֮����С����Ҫʹ����AC��BD�Ľ��㴦��
���������
��ͼ��ˮ��PӦ�����߶�AC���߶�BD�Ľ���P������������ƽ����ʡ����.
���ɣ����Dz�������ȡһ��P��,����AP�䡢BP��CP�䡢DP�䡢AB��BC��CD��DA��
�ߡ�AP��C��,AP��+CP��>AC=AP+CP...
˵��������.
����������������������߶ε����ʣ�����֮�䣬�߶ξ�����̣�������⣬Ҫʹ�����ĸ���ׯ�ľ���֮����С����Ҫʹ����AC��BD�Ľ��㴦��
���������
��ͼ��ˮ��PӦ�����߶�AC���߶�BD�Ľ���P������������ƽ����ʡ����.
���ɣ����Dz�������ȡһ��P��,����AP�䡢BP��CP�䡢DP�䡢AB��BC��CD��DA��
�ߡ�AP��C��,AP��+CP��>AC=AP+CP... �ڡ�ABC�У����߳��ֱ�Ϊ������a��b��c����c��b��a��0�����b=4���������������ι���_________����
 10
��������������������ڡ�ABC�У����߳��ֱ�Ϊ������a��b��c����
��c
10
��������������������ڡ�ABC�У����߳��ֱ�Ϊ������a��b��c����
��c���� 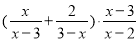 ��____________.
��____________.
 1
�����������ݷ�ʽ�Ļ�����㣬������������ģ�����˷����ɵ�===1.
�ʴ�Ϊ��1.
1
�����������ݷ�ʽ�Ļ�����㣬������������ģ�����˷����ɵ�===1.
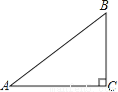
�ʴ�Ϊ��1. ��ͼ���ڡ�ABC�У���C��90�㣬AB��5��BC��3����sinA��ֵΪ�� ��
A. 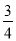 B.
B. 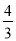 C.
C. 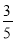 D.
D. 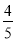
 C
�������������������Rt��ABC�У���C=90�㣬AC=3��BC=4��
�ɹ��ɶ�������
AB=��
cosA=��
��ѡA��
C
�������������������Rt��ABC�У���C=90�㣬AC=3��BC=4��
�ɹ��ɶ�������
AB=��
cosA=��
��ѡA�� 
