题目内容
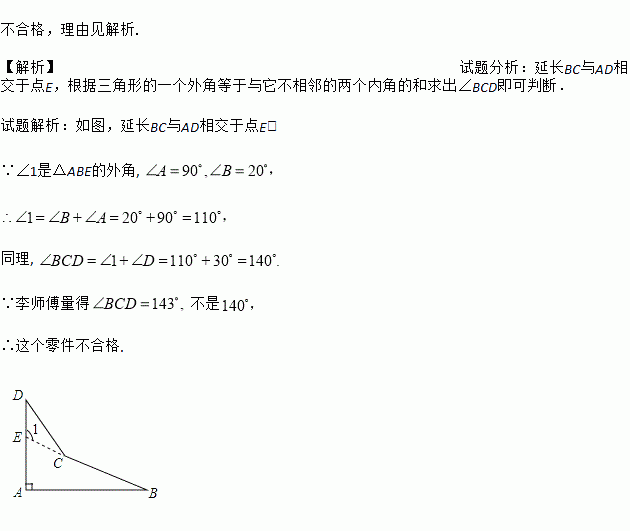
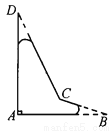
一个飞机零件的形状如图5—19所示，按规定∠A应等于90°，∠B，∠D应分别是20°和30°，康师傅量得∠BCD=143°，就能断定这个零件不合格，你能说出其中的道理吗?
不合格，理由见解析.
【解析】试题分析：延长BC与AD相交于点E，根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BCD即可判断．
试题解析：如图，延长BC与AD相交于点E，
∵∠1是△ABE的外角,
同理,
∵李师傅量得不是
∴这个零件不合格.
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目
已知：如图，AB∥CD，EF分别交于AB、CD于E、F，EG平分∠AEF，FH平分∠EFD。
求证： EG∥FH
证明：∵ AB∥CD（已知），∴ ∠AEF=∠EFD （______）。∵ EG平分∠AEF，FH平分∠EFD（______），∴∠______=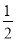
∠AEF，∠______=
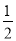∠EFD（角平分线定义）。∴ ∠______=∠______，∴ EG∥FH（______）。
两直线平行，内错角相等，已知，∠GEF，∠EFH，∠GEF，∠EFH，内错角相等，两直线平行。
【解析】试题分析：本题只要根据平行线的性质以及角平分线的性质得出角相等，最后根据内错角相等，两直线平行得出答案． 已知sinα＝0.8536，则α＝____度___分___秒．
58 36 19
【解析】试题解析：由sinα=0.853 6，用科学计算器求得α≈58.605 4°，
所以α≈58度36分19秒，
故答案为：58；36；19.
故答案为：58；36；19. 已知点A的坐标为（-2，3），点B的坐标为（0，1），则点A关于点B的坐标为（ ）
A. （ -2，2 ） B. （2，-3 ） C. （ 2，-1 ） D. （2，3 ）
C
【解析】因为点A的坐标为（-2,3）,点B的坐标为（0,1）,则点A关于点B的坐标为（2,-1）,故选C. △ABC中，三个内角的度数均为整数，且∠A＜∠B＜∠C，4∠C=7∠A，求∠A的度数．
44°
【解析】试题分析：先用∠A表示出∠C，再根据三角形的内角和等于180°列式整理用
∠A表示出∠B，再根据不等式求出∠A的取值范围，最后根据∠A是整数解答．
试题解析：
∵4∠C=7∠A，
∵∠A<∠B<∠C，
由①得,
由②得,
∵∠A,∠C是整数,
∴∠A是4的整数倍， 如图，△ABC中，∠A=60°，∠ABC、∠ACB的平分线BD、CD交于点D，则∠BDC=_____．
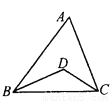
120°
【解析】试题解析：在△ABC中，
∵BD是∠ABC的平分线，CD是∠ACB的平分线，
在△BCI中，
故答案为： 一个三角形的三个内角的度数的比是2：2：1，这个三角形是_________三角形．
锐角（等腰锐角）
【解析】试题解析：一个三角形的三个内角的度数的比是2:2:1，则一定有两个角相等，则三角形是：等腰三角形，
底角一定大于顶角，则三角形一定是锐角三角形.
故答案是：锐角(等腰锐角). 若代数式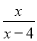
有意义，则实数
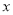的取值范围是（ ）
A. x=0 B. x=4 C. x≠0 D. x≠4
D
【解析】由分式有意义的条件:分母不为0，即x-4≠0，解得x≠4，
故选D. Rt△ABC中，∠C=90°，AB=10，BC=8，求cosB的值.
【解析】分析: 直接利用锐角三角函数关系得出cosB.
本题解析：
∵∠C=90°，AB=10，BC=8，
∴cosB=
故答案为：