题目内容
如图,在△ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm,求:(1)△ABC的面积;(2)CD的长.
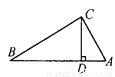
 (1)30cm2;(2) cm.
【解析】(1)根据直角三角形面积的求法,即可得出△ABC的面积,
(2)根据三角形的面积公式即可求得CD的长,
【解析】
(1)∵∠ACB=90°,BC=12cm,AC=5cm,
∴S△ABC=BC×AC=30cm2,
(2)∵S△ABC=AB×CD=30cm2,
∴CD=30÷AB=cm,
(1)30cm2;(2) cm.
【解析】(1)根据直角三角形面积的求法,即可得出△ABC的面积,
(2)根据三角形的面积公式即可求得CD的长,
【解析】
(1)∵∠ACB=90°,BC=12cm,AC=5cm,
∴S△ABC=BC×AC=30cm2,
(2)∵S△ABC=AB×CD=30cm2,
∴CD=30÷AB=cm,
练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
已知:如图,AB∥CD,BE∥CF。
求证:∠1=∠4。
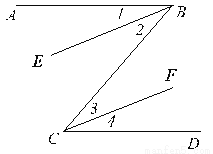
 证明见解析
【解析】试题分析:根据AB∥CD得出∠ABC=∠BCD,然后根据BE∥CF得出∠2=∠3,从而得出答案.
试题解析:∵AB∥CD(已知), ∴∠ABC=∠BCD(两条直线平行,内错角相等),
∵BE∥CF(已知),∴∠2=∠3(两条直线平行,内错角相等),
∵∠ABC=∠1+∠2,∠BCD=∠3+∠4,∴∠1=∠4.
证明见解析
【解析】试题分析:根据AB∥CD得出∠ABC=∠BCD,然后根据BE∥CF得出∠2=∠3,从而得出答案.
试题解析:∵AB∥CD(已知), ∴∠ABC=∠BCD(两条直线平行,内错角相等),
∵BE∥CF(已知),∴∠2=∠3(两条直线平行,内错角相等),
∵∠ABC=∠1+∠2,∠BCD=∠3+∠4,∴∠1=∠4. 如图,工作人员在一块长方体的铁块中挖掉了一部分,留下一个燕尾槽,上口宽AD为180mm,下口宽BC为278mm,槽深为70mm.求它的燕尾角.(精确到1°)
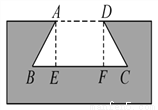
 55°
【解析】试题分析:过A作AE⊥BC与点E,则BC=AD+2BE,可求得BE的长,在直角中,根据三角函数,从而求解.
试题解析:作AE⊥BC于E,DF⊥BC于F,
所以
在中,
答:它的燕尾角为
55°
【解析】试题分析:过A作AE⊥BC与点E,则BC=AD+2BE,可求得BE的长,在直角中,根据三角函数,从而求解.
试题解析:作AE⊥BC于E,DF⊥BC于F,
所以
在中,
答:它的燕尾角为 点M(2,-3)与点N(2,3)关于______对称;点A(-2,-4)与点B(2,4)关于______对称;点G(4,0)与点H(-4,0)关于____________对称.
 x轴 原点 y轴
【解析】根据关于x轴对称的点的坐标规律:横坐标相同,纵坐标互为相反数,关于原点的对称点,横纵坐标都变成相反数,关于y轴对称的点的坐标规律:横坐标互为相反数,纵坐标相同,
所以点M与点N关于x轴对称,点A与点B关于原点对称,点G与点H关于y轴对称,故答案为: x轴, 原点, y轴.
x轴 原点 y轴
【解析】根据关于x轴对称的点的坐标规律:横坐标相同,纵坐标互为相反数,关于原点的对称点,横纵坐标都变成相反数,关于y轴对称的点的坐标规律:横坐标互为相反数,纵坐标相同,
所以点M与点N关于x轴对称,点A与点B关于原点对称,点G与点H关于y轴对称,故答案为: x轴, 原点, y轴. 已知a<0,则点P(-a2,-a+1)关于原点的对称点P′在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
 D
【解析】因为点P(-a2,-a+1)关于原点的对称点为P′,所以P′(a2,a-1),
又因为a<0,所以a-1<0,a2>0,所以P′在第四象限.故选D.
D
【解析】因为点P(-a2,-a+1)关于原点的对称点为P′,所以P′(a2,a-1),
又因为a<0,所以a-1<0,a2>0,所以P′在第四象限.故选D. 如图,点B、C、D、E共线,试问图中A、B、C、D、E五点可确定多少个三角形?说明理由.
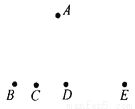
 6个.
【解析】试题分析:经过两点可以确定一条线段,而不在同一条直线上的三条线段首尾顺次相接可组成一个三角形,因而三角形的个数就是B、C、D、E四点中,两个分成一组,点的组数.
试题解析:可以确定6个三角形.
理由:经过两点可以确定一条线段,而不在同一条直线上的三条线段首尾顺次相接可组成一个三角形,
所以图中可以确定6个三角形.
6个.
【解析】试题分析:经过两点可以确定一条线段,而不在同一条直线上的三条线段首尾顺次相接可组成一个三角形,因而三角形的个数就是B、C、D、E四点中,两个分成一组,点的组数.
试题解析:可以确定6个三角形.
理由:经过两点可以确定一条线段,而不在同一条直线上的三条线段首尾顺次相接可组成一个三角形,
所以图中可以确定6个三角形. 直角三角形中,两个锐角的差为40°,则这两个锐角的度数分别为_________.
 65°和25°
【解析】试题解析:设这两个锐角的度数分别为x,y,
根据题意得,
解得
故答案为:
65°和25°
【解析】试题解析:设这两个锐角的度数分别为x,y,
根据题意得,
解得
故答案为: 已知a=b+2 018,求代数式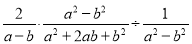 的值.
的值.
 4036
【解析】试题分析:根据分式的乘除法,先对分子分母分解因式,然后把除法化为乘法,再约分,然后代入求值.
试题解析:原式=××(a-b)(a+b)=2(a-b).
∵a=b+2 018,∴原式=2×2 018=4 036.
4036
【解析】试题分析:根据分式的乘除法,先对分子分母分解因式,然后把除法化为乘法,再约分,然后代入求值.
试题解析:原式=××(a-b)(a+b)=2(a-b).
∵a=b+2 018,∴原式=2×2 018=4 036. 如图所示,△ 的顶点是正方形网格的格点,则sin
的顶点是正方形网格的格点,则sin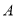 的值为( )
的值为( )
A. 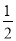 B.
B. 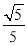 C.
C. 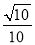 D.
D. 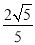
 B
【解析】直接根据题意构造直角三角形,进而利用勾股定理得出DC,AC的长,再利用锐角三角函数关系求出答案.
【解析】
如图所示:连接DC,
由网格可得出∠CDA=90°,
则DC=,AC=,
故sinA===.
故选B.
“点睛”此题主要考查了勾股定理以及锐角三角函数关系,正确构造直角三角形是解题关键.
B
【解析】直接根据题意构造直角三角形,进而利用勾股定理得出DC,AC的长,再利用锐角三角函数关系求出答案.
【解析】
如图所示:连接DC,
由网格可得出∠CDA=90°,
则DC=,AC=,
故sinA===.
故选B.
“点睛”此题主要考查了勾股定理以及锐角三角函数关系,正确构造直角三角形是解题关键. 
