题目内容
如图，在△ABC中，AD是BC边上的中线，△ADC的周长比△ABD的周长多5cm，AB与AC的和为11cm，求AC的长．
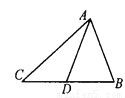
8cm.
【解析】试题分析：根据中线的定义知CD=BD，结合三角形的周长公式知AC﹣AB=5cm，又AB+AC=11cm，易求AC的长度.
试题解析：∵AD是BC边上的中线，
∴D为BC的中点，CD=BD．
∵△ADC的周长﹣△ABD的周长=5cm．
∴AC﹣AB=5cm．
又∵AB+AC=11cm，
∴AC=8cm．即AC的长度是8cm．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知：如图，∠1=35º，AB⊥CD，垂足为O，EF经过点O。求∠2、∠3、∠4的度数。
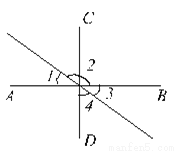
∠2=145°，∠3=35°， ∠4=55°
【解析】试题分析：首先根据对顶角的性质得出∠3的度数，根据邻补角的性质求出∠2的度数，最后根据垂直的定义求出∠4的度数．
试题解析：∵∠1和∠3是对顶角， ∴∠3=∠1=35°， ∵∠1+∠2=180°，
∴∠2=180°-∠1=180°-35°=145°， ∵AB⊥CD， ∴∠3+∠4=90°，
∴∠4=90°-∠3=90°-... 如图，某河道要建造一座公路桥，要求桥面离地面高度AC为3米，该桥的坡角∠ABC为15°，则该桥的水平距离BC的长是___米(精确到0.1米)．
11.2
【解析】试题解析：Rt△ABC中,
(米).
故答案为：11.2. 点P（x，y）关于x轴对称的点P1为______；关于y轴对称的点P2为______；关于原点的对称点P3为______.
（x，-y） （-x，y） （-x，-y）
【解析】点P（x,y）关于x轴对称的点P1为 （x，-y）,关于y轴对称的点P2为 （-x,y）,关于原点的对称点P3为（-x，-y）,故答案为:（x,-y）,（-x,y）,（-x,-y）. 已知：如图，P是△ABC内任一点，求证：AB＋AC＞BP＋PC．
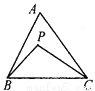
证明见解析.
【解析】试题分析：延长BP交AC于点D，由三角形的三边关系可得AB+AD＞BD，PD+DC＞PC，
试题解析：如图，延长BP交AC于点D.
在△ABD中，根据三边关系可得：
∵BD=BP+DP，
∴AB+AD＞BP+DP.
在△PCD中，根据三边关系可得：PD+DC＞PC， 如图，该五角星中，∠A＋∠B＋∠C＋∠D＋∠E=________度．
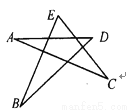
180°
【解析】试题解析：如图所示：
∵∠DGE是△EGB的外角，∴∠DGF=∠B+∠E，
∵∠DFG是△AFC的外角，∴∠DFG=∠A+∠C，
∵∠DFG+∠DGF+∠D=
∴∠A+∠B+∠C+∠D+∠E=
故答案是：180. 一个等腰三角形两边的长分别是15cm和7cm则它的周长是__________．
37cm
【解析】①7cm是腰长时，三角形的三边分别为7cm、7cm、15cm，
∵7+7=14<15，
∴不能组成三角形，
②7cm是底边时，三角形的三边分别为7cm、15cm、15cm，
能组成三角形，
周长=7+15+15=37cm，
综上所述，它的周长是37cm.
故答案为：37cm. 计算：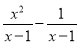 
＝____________.
.x＋1
【解析】试题分析：根据同分母分式相加减，再因式分解后约分即可得： ==x+1.
故答案为：x+1. 在Rt△ABC中，∠C=90°，如果AC：BC=3：4，求cosA的值.
【解析】分析:根据题意设AC=3x，BC=4x，故AB=5x，进而利用锐角三角函数关系求出答案．
本题解析：
∵在Rt△ABC中，∠C=90°，AC：BC=3：4，
∴设AC=3x，BC=4x，故AB=5x，
则cosA=
故答案为：