题目内容
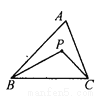
已知:如图,P是△ABC内任一点,求证:∠BPC>∠A.
 说明见解析.
【解析】试题分析:延长BP交AC于D. 根据△PDC外角的性质知∠BPC>∠PDC,根据△ABD外角的性质知∠PDC>∠A,所以易证∠BPC>∠A.
试题解析:如图,延长BP交AC于D.
∵∠BPC>∠PDC,∠PDC>∠A,
∴∠BPC>∠A.
说明见解析.
【解析】试题分析:延长BP交AC于D. 根据△PDC外角的性质知∠BPC>∠PDC,根据△ABD外角的性质知∠PDC>∠A,所以易证∠BPC>∠A.
试题解析:如图,延长BP交AC于D.
∵∠BPC>∠PDC,∠PDC>∠A,
∴∠BPC>∠A.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
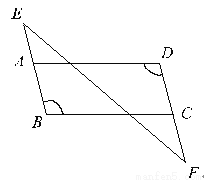
已知:如图,BE∥DF,∠B=∠D。求证:AD∥BC。
 证明见解析
【解析】试题分析:根据BE∥DF得出∠D=∠EAD,结合已知条件得出∠B=∠EAD,从而根据同位角相等两直线平行得出答案.
试题解析:∵BE∥DF(已知),∴∠D=∠EAD(两条直线平行,内错角相等),
∵∠B=∠D(已知),∴∠B=∠EAD,∴AD∥BC(同位角相等,两直线平行).
证明见解析
【解析】试题分析:根据BE∥DF得出∠D=∠EAD,结合已知条件得出∠B=∠EAD,从而根据同位角相等两直线平行得出答案.
试题解析:∵BE∥DF(已知),∴∠D=∠EAD(两条直线平行,内错角相等),
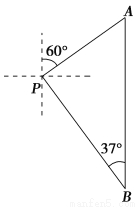
∵∠B=∠D(已知),∴∠B=∠EAD,∴AD∥BC(同位角相等,两直线平行). 周末,小亮一家在东昌湖游玩,妈妈在湖心岛岸边P处观看小亮与爸爸在湖中划船(如图).小船从P处出发,沿北偏东60°划行200米到达A处,接着向正南方向划行一段时间到达B处.在B处小亮观测妈妈所在的P处在北偏西37°方向上,这时小亮与妈妈相距多少米(精确到米)?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,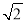 ≈1.41,
≈1.41,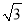 ≈1.73)
≈1.73)
 288米
【解析】
【解析】
作PD⊥AB于点D,
由已知得PA=200米,∠APD=30°,∠B=37°,
在Rt△PAD中,
由cos30°=,得PD=PAcos30°=200×=100米,
在Rt△PBD中,由sin37°=,
得PB=≈≈288米.
答:小亮与妈妈的距离约为288米.
288米
【解析】
【解析】
作PD⊥AB于点D,
由已知得PA=200米,∠APD=30°,∠B=37°,
在Rt△PAD中,
由cos30°=,得PD=PAcos30°=200×=100米,
在Rt△PBD中,由sin37°=,
得PB=≈≈288米.
答:小亮与妈妈的距离约为288米. 直线y=x+3上有一点P(3,n),则点P关于原点的对称点P′为________.
 P′为(-3,-6)
【解析】因为直线y=x+3上有一点P(3,n),所以n=3+3=6,所以P(3,6),所以点P关于原点的对称点P′为(-3,-6),故答案为:(-3,-6).
P′为(-3,-6)
【解析】因为直线y=x+3上有一点P(3,n),所以n=3+3=6,所以P(3,6),所以点P关于原点的对称点P′为(-3,-6),故答案为:(-3,-6). 设点A与点B关于x轴对称,点A与点C关于y轴对称,则点B与点C( )
A. 关于x轴对称 B. 关于y轴对称 C. 关于原点对称. D. 既关于x轴对称,又关于y轴对称
 C
【解析】根据关于x轴对称的点的坐标规律:横坐标相同,纵坐标互为相反数,关于原点的对称点,横纵坐标都变成相反数,关于y轴对称的点的坐标规律:横坐标互为相反数,纵坐标相同,
点A与点B关于x轴对称,点A与点C关于y轴对称,则点B与点C原点对称,故选C.
C
【解析】根据关于x轴对称的点的坐标规律:横坐标相同,纵坐标互为相反数,关于原点的对称点,横纵坐标都变成相反数,关于y轴对称的点的坐标规律:横坐标互为相反数,纵坐标相同,
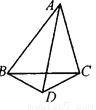
点A与点B关于x轴对称,点A与点C关于y轴对称,则点B与点C原点对称,故选C. 如图,∠BAD=∠CAD,则AD是△ABC的角平分线,对吗?说明理由.
 不是,理由见解析.
【解析】试题分析:考查了三角形的角平分线的定义,三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线.
试题解析:根据三角形的角平分线的定义,可知:①平分三角形的一个内角;②是一条线段,一个端点是三角形的顶点,另一点在这个顶点的对边上.而此题中AD满足①,但点D不在BC边上,故不满足②.所以,AD不是△ABC的角平分...
不是,理由见解析.
【解析】试题分析:考查了三角形的角平分线的定义,三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线.
试题解析:根据三角形的角平分线的定义,可知:①平分三角形的一个内角;②是一条线段,一个端点是三角形的顶点,另一点在这个顶点的对边上.而此题中AD满足①,但点D不在BC边上,故不满足②.所以,AD不是△ABC的角平分... 在△ABC中,∠A-∠B=30°、∠C=4∠B,则∠C=________.
 100°
【解析】试题解析:
①,
②,
①?②得, 解得
故答案为:
100°
【解析】试题解析:
①,
②,
①?②得, 解得
故答案为: 先化简,再求值:(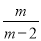 –
–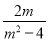 )÷
)÷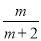 ,请在2,–2,0,3当中选一个合适的数代入求值.
,请在2,–2,0,3当中选一个合适的数代入求值.
 ,当m=3时,原式=3.
【解析】试题分析:括号内分式通分后相减,再把除法转化为乘法,分母分解因式后约分,然后再从给出的四个数中选择能使原分式有意义的值代入计算即可.
试题解析:
【解析】
原式=
=
=,
当m=3时,
原式==3.
,当m=3时,原式=3.
【解析】试题分析:括号内分式通分后相减,再把除法转化为乘法,分母分解因式后约分,然后再从给出的四个数中选择能使原分式有意义的值代入计算即可.
试题解析:
【解析】
原式=
=
=,
当m=3时,
原式==3. 如图,点A为∠α边上任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )
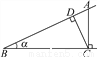
A. 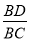 B.
B. 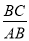 C.
C. 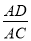 D.
D. 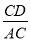
 C
【解析】∵AC⊥BC,CD⊥AB,
∴∠α+∠BCD=∠ACD+∠BCD,
∴∠α=∠ACD,
∴cosα=cos∠ACD===,
只有选项C错误.
故选C.
C
【解析】∵AC⊥BC,CD⊥AB,
∴∠α+∠BCD=∠ACD+∠BCD,
∴∠α=∠ACD,
∴cosα=cos∠ACD===,
只有选项C错误.
故选C. 
