如图,已知线段AB的垂直平分线CP交AB于点P,且AP=2PC,现欲在线段AB上求作两点D,E,使其满足AD=DC=CE=EB,对于以下甲、乙两种作法:
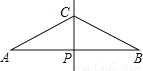
甲:分别作∠ACP、∠BCP的平分线,分别交AB于D、E,则D、E即为所求;乙:分别作AC、BC的垂直平分线,分别交AB于D、E,则D、E两点即为所求.下列说法正确的是( )
A. 甲、乙都正确 B. 甲、乙都错误
C. 甲正确,乙错误 D. 甲错误,乙正确
 D
【解析】试题解析:甲:虽然CP=AP,
但∠A≠∠ACP,
即∠A≠∠ACD.甲不正确;
乙∵CP是线段AB的中垂线,
∴△ABC是等腰三角形,即AC=BC,∠A=∠B,
作AC、BC之中垂线分别交AB于D、E,
∴∠A=∠ACD,∠B=∠BCE,
∵∠A=∠B,
∴∠A=∠ACD,∠B=∠BCE,
∵AC=BC,
∴△ACD≌...
D
【解析】试题解析:甲:虽然CP=AP,
但∠A≠∠ACP,
即∠A≠∠ACD.甲不正确;
乙∵CP是线段AB的中垂线,
∴△ABC是等腰三角形,即AC=BC,∠A=∠B,
作AC、BC之中垂线分别交AB于D、E,
∴∠A=∠ACD,∠B=∠BCE,
∵∠A=∠B,
∴∠A=∠ACD,∠B=∠BCE,
∵AC=BC,
∴△ACD≌... 利用尺规作三角形的三条边的垂直平分线,观察这三条垂直平分线的位置关系,你发现了什么?再换一个三角形试一试.
 见解析
【解析】试题分析:运用尺规作图作出三角形的三条边的垂直平分线,找出这三条垂直平分线的位置关系即可.
试题解析:三角形的三条边的垂直平分线相交于一点.
见解析
【解析】试题分析:运用尺规作图作出三角形的三条边的垂直平分线,找出这三条垂直平分线的位置关系即可.
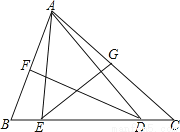
试题解析:三角形的三条边的垂直平分线相交于一点. 如图,在△ABC中,∠C=40°,∠B=68°,AB、AC的垂直平分线分别交BC于D、E.求∠EAD的度数.
 36°
【解析】试题分析:根据三角形内角和定理求出∠BAC的度数,根据线段的垂直平分线的性质得到DA=DB,EA=EC,根据等腰三角形的性质分别求出∠DAC和∠BAE的度数,计算得到∠EAD的度数.
试题解析:∵∠C=40°,∠B=68°,
∴∠BAC=72°,
∵DF是线段AB的垂直平分线,
∴DA=DB,
∴∠DAB=∠B=68°,
∴∠DAC=4°,...
36°
【解析】试题分析:根据三角形内角和定理求出∠BAC的度数,根据线段的垂直平分线的性质得到DA=DB,EA=EC,根据等腰三角形的性质分别求出∠DAC和∠BAE的度数,计算得到∠EAD的度数.
试题解析:∵∠C=40°,∠B=68°,
∴∠BAC=72°,
∵DF是线段AB的垂直平分线,
∴DA=DB,
∴∠DAB=∠B=68°,
∴∠DAC=4°,... 在△ABC中,AB=AC,BC=12,∠B=30°,AB的垂直平分线DE交BC边于点E,AC的垂直平分线MN交BC于点N.
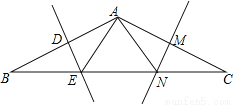
(1)求△AEN的周长;
(2)求证:BE=EN=NC.
 (1)12;(2)见解析
【解析】试题分析:(1)根据线段的垂直平分线的性质得到EB=EA,NA=NC,根据三角形的周长公式计算即可;
(2)根据等腰三角形的性质和三角形的外角的性质证明△AEN是等边三角形,等量代换证明即可.
试题解析:(1)∵DE是AB的垂直平分线,
∴EB=EA,
∵MN是AC的垂直平分线,
∴NA=NC,
则△AEN的周长=AE+A...
(1)12;(2)见解析
【解析】试题分析:(1)根据线段的垂直平分线的性质得到EB=EA,NA=NC,根据三角形的周长公式计算即可;
(2)根据等腰三角形的性质和三角形的外角的性质证明△AEN是等边三角形,等量代换证明即可.
试题解析:(1)∵DE是AB的垂直平分线,
∴EB=EA,
∵MN是AC的垂直平分线,
∴NA=NC,
则△AEN的周长=AE+A... 如图,已知在△ABC中,∠C=90°,AB的垂直平分线MN交BC于点D.
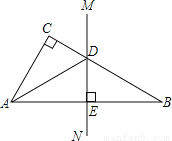
(1)如果∠CAD=20°,求∠B的度数;
(2)如果∠CAB=50°,求∠CAD的度数;
(3)如果∠CAD:∠DAB=1:2,求∠CAB的度数.
 (1)∠B=35°;(2)∠CAD=10°;(3)∠CAB=54°.
【解析】试题分析:(1)根据直角三角形的性质求出∠ADC=70°,根据线段的垂直平分线的性质得到DA=DB,计算即可;
(2)根据直角三角形的性质求出∠B的度数,根据线段的垂直平分线的性质得到DA=DB,计算即可;
(3)设∠CAD=x,根据题意列出方程,解方程即可.
试题解析:(1)∵∠C=90°,∠C...
(1)∠B=35°;(2)∠CAD=10°;(3)∠CAB=54°.
【解析】试题分析:(1)根据直角三角形的性质求出∠ADC=70°,根据线段的垂直平分线的性质得到DA=DB,计算即可;
(2)根据直角三角形的性质求出∠B的度数,根据线段的垂直平分线的性质得到DA=DB,计算即可;
(3)设∠CAD=x,根据题意列出方程,解方程即可.
试题解析:(1)∵∠C=90°,∠C... 如图,△ABC中,D、E在AB上,且D、E分别是AC、BC的垂直平分线上一点.
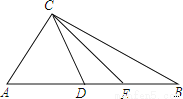
(1)若△CDE的周长为4,求AB的长;
(2)若∠ACB=100°,求∠DCE的度数;
(3)若∠ACB=a(90°<a<180°),则∠DCE=___________.
 (1)4;(2)20°;(3)2α-180°.
【解析】试题分析:(1)根据线段的垂直平分线的性质得到DC=DA,EC=EB,根据三角形的周长公式计算即可;
(2)根据三角形内角和定理求出∠A+∠B的度数,根据等腰三角形的性质求出∠DCA+∠ECB,根据题意计算即可;
(3)根据(2)的方法解答.
试题解析:(1)∵D、E分别是AC、BC的垂直平分线上一点,
∴DC=...
(1)4;(2)20°;(3)2α-180°.
【解析】试题分析:(1)根据线段的垂直平分线的性质得到DC=DA,EC=EB,根据三角形的周长公式计算即可;
(2)根据三角形内角和定理求出∠A+∠B的度数,根据等腰三角形的性质求出∠DCA+∠ECB,根据题意计算即可;
(3)根据(2)的方法解答.
试题解析:(1)∵D、E分别是AC、BC的垂直平分线上一点,
∴DC=... 如图,下列说法正确的是 ( )
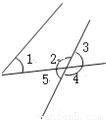
A. ∠1和∠2是内错角 B. ∠1和∠3是内错角
C. ∠1和∠4是内错角 D. ∠1和∠5是内错角
 D
【解析】A. ∵∠1和∠2是同旁内角,故不正确;
B. ∵∠1和∠3是同位角,故不正确;
C. ∵ ∠1和∠4不具备特殊位置关系,故不正确;
D. ∵∠1和∠5是内错角,故正确;
故选D.
D
【解析】A. ∵∠1和∠2是同旁内角,故不正确;
B. ∵∠1和∠3是同位角,故不正确;
C. ∵ ∠1和∠4不具备特殊位置关系,故不正确;
D. ∵∠1和∠5是内错角,故正确;
故选D. 如图,与∠B是同旁内角的角有( )
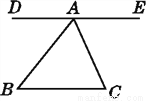
A. 1个 B. 2个 C. 3个 D. 4个
 C
【解析】与∠B是同旁内角的角有∠C, ∠BAC, ∠BAE共3个.
故选C.
C
【解析】与∠B是同旁内角的角有∠C, ∠BAC, ∠BAE共3个.
故选C. 如图,点E在BC的延长线上,下列条件中能判定BC//AD的是 ( )
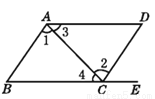
A. ∠1=∠2 B. ∠DAB+∠D=180° C. ∠3=∠4 D. ∠B=∠DCE
 C
【解析】A. ∵∠1=∠2 ,∴AB∥CD, 故不正确;
B. ∵ ∠DAB+∠D=180° ,∴AB∥CD, 故不正确;
C. ∵∠3=∠4 ,∴ BC∥AD, 故正确;
D. ∵∠B=∠DCE,∴AB∥CD, 故不正确;
故选C.
C
【解析】A. ∵∠1=∠2 ,∴AB∥CD, 故不正确;
B. ∵ ∠DAB+∠D=180° ,∴AB∥CD, 故不正确;
C. ∵∠3=∠4 ,∴ BC∥AD, 故正确;
D. ∵∠B=∠DCE,∴AB∥CD, 故不正确;
故选C. 下列图形中,由∠1=∠2能得到AB∥CD的是( )
A. 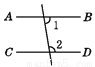 B.
B. 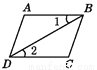 C.
C. 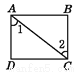 D.
D. 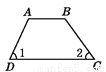
 B
【解析】试题分析:利用平行线的判定方法判断即可.
【解析】
如图所示:
∵∠1=∠2(已知),
∴AB∥CD(内错角相等,两直线平行),
故选B
B
【解析】试题分析:利用平行线的判定方法判断即可.
【解析】
如图所示:
∵∠1=∠2(已知),
∴AB∥CD(内错角相等,两直线平行),
故选B