题目内容
如图，点E在BC的延长线上，下列条件中能判定BC//AD的是 ( )
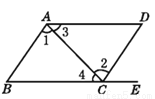
A. ∠1=∠2 B. ∠DAB+∠D=180° C. ∠3=∠4 D. ∠B=∠DCE
C
【解析】A. ∵∠1=∠2 ，∴AB∥CD, 故不正确；
B. ∵ ∠DAB+∠D=180° ，∴AB∥CD, 故不正确；
C. ∵∠3=∠4 ，∴ BC∥AD, 故正确；
D. ∵∠B=∠DCE，∴AB∥CD, 故不正确；
故选C.
练习册系列答案
课课练江苏系列答案
名牌中学课时作业系列答案
相关题目
小明统计了他家今年5月份打电话的次数及通话时间,并列出了如下的频数分布表:
通话时间 x/min | 0<x≤5 | 5<x≤10 | 10<x≤15 | 15<x≤20 |
频数 (通话次数) | 20 | 16 | 9 | 5 |
则通话时间不超过15 min的频率为( )
A. 0.1 B. 0.4 C. 0.5 D. 0.9
D
【解析】用不超过15分钟的通话时间除以所有的通话时间即可求得通话时间不超过15分钟的频率．
【解析】
∵不超过15分钟的通话次数为20+16+9=45次，通话总次数为20+16+9+5=50次，
∴通话时间不超过15min的频率为=0.9，
故选D．
“点睛”本题考查了频数分布表的知识，解题的关键是了解频率=频数÷样本容量，难度不大． 如图,已知∠A+∠ACD+∠D=360°,试说明:AB∥DE.
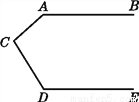
证明见解析.
【解析】试题分析：过点C作CF∥AB，结合已知可得∠A+∠ACF=180°，再根据已知角关系可得∠D+∠FCD=180°，根据平行线的判定即可得到CF∥DE，此时再次运用平行线的判定即可解答本题.
试题解析：过点C作CF∥AB.
∵CF∥AB，
∴∠A+∠ACF=180°.
∵∠A+∠ACD+∠D=360°，
∴∠D+∠FCD=180°，
∴... 如图,两只手的食指和大拇指在同一个平面内,它们构成的一对角可看成是___.
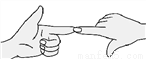
内错角
【解析】图中两只手的食指和拇指构成”Z“形，根据内错角是在截线两旁，被截线之内的两角，内错角的边构成”Z“形，可知答案为：内错角.
故答案为：内错角. 如图，∠1和∠2是直线_______和直线________被直线______所截得的同位角；
∠1和∠3是直线_______和直线________被直线______所截得的__________角；
∠2和∠4是直线_______和直线________被直线______所截得的__________角；
∠3和∠4是直线_______和直线________被直线______所截得的__________角；
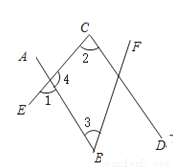
AB，CD，CE；CE，BF，AB,内错；AB，CD，CE，同旁内；CE，BF，AB，同旁内
【解析】如图，∠1和∠2是直线AB和直线CD被直线CE所截得的同位角；
∠1和∠3是直线CE和直线BF被直线AB所截得的内错角；
∠2和∠4是直线AB和直线CD被直线CE所截得的同旁内角；
∠3和∠4是直线CE和直线BF被直线AB所截得的同旁内角； 在△ABC中，AB=AC，BC=12，∠B=30°，AB的垂直平分线DE交BC边于点E，AC的垂直平分线MN交BC于点N.
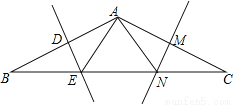
（1）求△AEN的周长；
（2）求证：BE=EN=NC.
（1）12；（2）见解析
【解析】试题分析：（1）根据线段的垂直平分线的性质得到EB=EA，NA=NC，根据三角形的周长公式计算即可；
（2）根据等腰三角形的性质和三角形的外角的性质证明△AEN是等边三角形，等量代换证明即可．
试题解析：（1）∵DE是AB的垂直平分线，
∴EB=EA，
∵MN是AC的垂直平分线，
∴NA=NC，
则△AEN的周长=AE+A... 到三角形三个顶点的距离都相等的点是这个三角形的（ ）
A. 三条高的交点 B. 三条角平分线的交点
C. 三条中线的交点 D. 三条边的垂直平分线的交点
D
【解析】【解析】
到三角形三个顶点的距离都相等的点是这个三角形的三条边的垂直平分线的交点，故选D． 已知在△ABC中，∠ABC=∠ACB，∠1=∠2，求证：AD平分∠BAC。
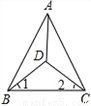
证明见解析
【解析】试题分析：易证AB=AC和BD=CD，即可证明△ABD≌△ACD，可得∠BAD=∠CAD，即可解题．
试题解析：∵∠ABC=∠ACB，
∴AB=AC，
∵∠1=∠2，
∴BD=CD，
在△ABD和△ACD中，
，
∴△ABD≌△ACD（SSS），
∴∠BAD=∠CAD，
∴AD平分∠BAC. 如图，AB∥FC，DE＝EF，AB＝15，CF＝8，则BD等于( )
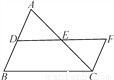
A. 8 B. 7 C. 6 D. 5
B
【解析】∵AB//CF，
∴∠A=∠ECF，
又∵DE=EF，∠AED=∠CEF，
∴△ADE≌△CFE，
∴AD=CF=8，
∴BD=AB-AD=15-8=7，
故选B.