题目内容
如图,已知在△ABC中,∠C=90°,AB的垂直平分线MN交BC于点D.
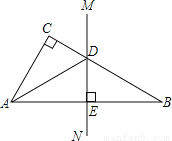
(1)如果∠CAD=20°,求∠B的度数;
(2)如果∠CAB=50°,求∠CAD的度数;
(3)如果∠CAD:∠DAB=1:2,求∠CAB的度数.
 (1)∠B=35°;(2)∠CAD=10°;(3)∠CAB=54°.
【解析】试题分析:(1)根据直角三角形的性质求出∠ADC=70°,根据线段的垂直平分线的性质得到DA=DB,计算即可;
(2)根据直角三角形的性质求出∠B的度数,根据线段的垂直平分线的性质得到DA=DB,计算即可;
(3)设∠CAD=x,根据题意列出方程,解方程即可.
试题解析:(1)∵∠C=90°,∠C...
(1)∠B=35°;(2)∠CAD=10°;(3)∠CAB=54°.
【解析】试题分析:(1)根据直角三角形的性质求出∠ADC=70°,根据线段的垂直平分线的性质得到DA=DB,计算即可;
(2)根据直角三角形的性质求出∠B的度数,根据线段的垂直平分线的性质得到DA=DB,计算即可;
(3)设∠CAD=x,根据题意列出方程,解方程即可.
试题解析:(1)∵∠C=90°,∠C...
 名校课堂系列答案
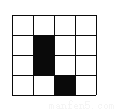
名校课堂系列答案如图是4×4正方形网络,其中已有3个小方格涂成了黑色。现在要从其余13个白色小方格中选出一个也涂成黑色的图形成为轴对称图形,这样的白色小方格有________个.
 4
【解析】试题分析:根据轴对称图形的概念分别找出各个能成轴对称图形的小方格即可.如图所示,有4个位置使之成为轴对称图形.
故答案为:4.
4
【解析】试题分析:根据轴对称图形的概念分别找出各个能成轴对称图形的小方格即可.如图所示,有4个位置使之成为轴对称图形.
故答案为:4. 如图,已知AB⊥BC,DC⊥BC,∠1=∠2,可得到BE∥CF,说明过程如下,请填上说明的依据:

因为AB⊥BC,DC⊥BC,
所以∠ABC=90°,
∠BCD=90°(______________),
所以∠ABC=∠BCD.
又因为∠1=∠2,
所以∠EBC=∠FCB.
所以BE∥CF(______________).
 垂直的定义;内错角相等,两直线平行
【解析】试题分析:题中已知AB⊥BC,DC⊥BC,根据垂直的定义可得∠ABC=∠BCD=90°,又因为∠1=∠2,由等量减等量,差相等可得∠EBC=∠FCB,观察图形可知,∠EBC与∠FCB是直线BE与CF被直线BC所截的内错角,即可得证.
试题解析:因为AB⊥BC,DC⊥BC(已知),
所以∠ABC=∠BCD=90°(垂直的定义).
又...
垂直的定义;内错角相等,两直线平行
【解析】试题分析:题中已知AB⊥BC,DC⊥BC,根据垂直的定义可得∠ABC=∠BCD=90°,又因为∠1=∠2,由等量减等量,差相等可得∠EBC=∠FCB,观察图形可知,∠EBC与∠FCB是直线BE与CF被直线BC所截的内错角,即可得证.
试题解析:因为AB⊥BC,DC⊥BC(已知),
所以∠ABC=∠BCD=90°(垂直的定义).
又... 已知:如图:∠1=∠2,∠3+∠4= 180°;确定直线a,c的位置关系,并说明理由;
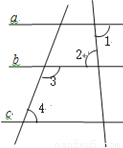
【解析】
a c;
理由:∵∠1=∠2( ),
∴ a // ( );
∵ ∠3+∠4= 180°( ),
∴ c // ( );
∵ a // ,c // ,
∴ // ( );
 答案见解析
【解析】试题分析:本题考查的是同学们对于平行线的判定的运用能力,内错角相等的两条直线平行;同旁内角互补的两条直线平行;平行于同一条直线的两条直线平行.
【解析】
a // c;
理由:∵∠1=∠2( 已知 ),
∴ a // b ( 内错角相等,两直线平行 );
∵ ∠3+∠4= 180°( 已知 ),
∴ c // b ( 同旁内角互补, 两直线...
答案见解析
【解析】试题分析:本题考查的是同学们对于平行线的判定的运用能力,内错角相等的两条直线平行;同旁内角互补的两条直线平行;平行于同一条直线的两条直线平行.
【解析】
a // c;
理由:∵∠1=∠2( 已知 ),
∴ a // b ( 内错角相等,两直线平行 );
∵ ∠3+∠4= 180°( 已知 ),
∴ c // b ( 同旁内角互补, 两直线... 下列图形中,由∠1=∠2能得到AB∥CD的是( )
A. 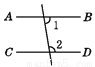 B.
B. 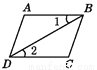 C.
C. 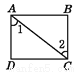 D.
D. 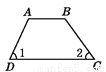
 B
【解析】试题分析:利用平行线的判定方法判断即可.
【解析】
如图所示:
∵∠1=∠2(已知),
∴AB∥CD(内错角相等,两直线平行),
故选B
B
【解析】试题分析:利用平行线的判定方法判断即可.
【解析】
如图所示:
∵∠1=∠2(已知),
∴AB∥CD(内错角相等,两直线平行),
故选B 已知△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是70cm和48cm,则△ABC的腰和底边长分别为( )
A.24cm和22cm B.26cm和18cm
C.22cm和26cm D.23cm和24cm
 C
【解析】
试题分析:根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD,然后求出△DBC的周长=AC+BC,再根据两个三角形的周长求出AB,然后BC的值即可.
【解析】
∵AB的垂直平分线交AC于D,
∴AD=BD,
∴△DBC的周长=BD+CD+BC=AD+CD+BC=AC+BC,
∵△ABC和△DBC的周长分别是70cm和48cm,
∴...
C
【解析】
试题分析:根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD,然后求出△DBC的周长=AC+BC,再根据两个三角形的周长求出AB,然后BC的值即可.
【解析】
∵AB的垂直平分线交AC于D,
∴AD=BD,
∴△DBC的周长=BD+CD+BC=AD+CD+BC=AC+BC,
∵△ABC和△DBC的周长分别是70cm和48cm,
∴... 如图,在△ABC中,D为AB的中点,AD=5 cm,∠B=∠C,BC=8 cm.
(1)若点P在线段BC上以3 cm/s的速度从点B向终点C运动,同时点Q在线段CA上从点C向终点A运动.
①若点Q的速度与点P的速度相等,经过1 s后,请说明△BPD≌△CQP.
②若点Q的速度与点P的速度不等,当点Q的速度为多少时,能使△BPD≌△CPQ?
(2)若点P以3 cm/s的速度从点B向点C运动,同时点Q以5 cm/s的速度从点C向点A运动,它们都依次沿△ABC三边运动,则经过多长时间,点Q第一次在△ABC的哪条边上追上点P?

 (1)说明见解析;(2)当点Q的运动速度为cm/s时,能使△BPD≌△CPQ.(3)10s.
【解析】试题分析:(1)①根据等腰三角形的性质得到∠B=∠C,再加上BP=CQ=3,PC=BD=5,则可判断△BPD与△CQP全等;
②设点Q的运动速度为xcm/s,则BP=3t,CQ=xt,CP=8-3t,当△BPD≌△CQP,则BP=CQ,CP=BD;然后分别建立关于t和v的方程,再解方程...
(1)说明见解析;(2)当点Q的运动速度为cm/s时,能使△BPD≌△CPQ.(3)10s.
【解析】试题分析:(1)①根据等腰三角形的性质得到∠B=∠C,再加上BP=CQ=3,PC=BD=5,则可判断△BPD与△CQP全等;
②设点Q的运动速度为xcm/s,则BP=3t,CQ=xt,CP=8-3t,当△BPD≌△CQP,则BP=CQ,CP=BD;然后分别建立关于t和v的方程,再解方程... 如图是5×5的正方形网络,以点D,E为两个顶点作位置不同的格点三角形,使所作的格点三角形与△ABC全等,这样的格点三角形最多可以画出( )
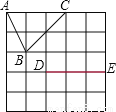
A. 2个 B. 4个 C. 6个 D. 8个
 B
【解析】如图,根据题意,运用SSS可得与△ABC全等的三角形有4个,线段DE的上方和下方各有两个符合的点,共4个.
故选:A.
B
【解析】如图,根据题意,运用SSS可得与△ABC全等的三角形有4个,线段DE的上方和下方各有两个符合的点,共4个.
故选:A. 杨辉三角是一个由数字排列成昀三角形数表,一般形式如图所示,其中每一横行都表示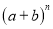 (此处
(此处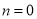 ,
, 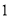 ,
, 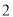 ,
, 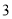 ,
, 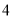 ,
, 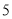 ,
, 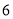 )的展开式中的系数,杨辉三角最本质的特征是,它的两条斜边都是由数字
)的展开式中的系数,杨辉三角最本质的特征是,它的两条斜边都是由数字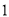 组成的,而其余的数则是等于它“肩”上的两个数之和.
组成的,而其余的数则是等于它“肩”上的两个数之和.
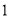
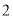
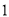
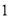
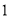
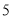
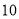
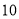
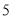
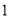
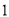
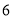
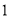
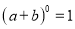
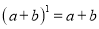
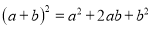
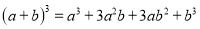
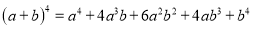
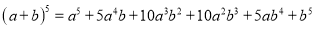
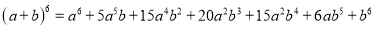
上图的构成规律你看懂了吗?
请你直接写出(a+b)7 =______.
杨辉三角还有另一个特征
(1)从第二行到第五行,每一行数字组成的数(如第三行为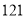 )都是上一行的数与______积.
)都是上一行的数与______积.
(2)由此你可写出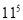 =______.
=______.
(3)由第_____行可写出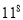 =______.
=______.
 (1)11 (2)161051 (3)9;214358881
【解析】试题分析:观察图表寻找规律:三角形是一个有数字排列形成的三角形数表,它的两条斜边都是数字1组成,而其余的数则是等于它“肩”上的两个数之和.
试题解析:
(1)从第二行到第五行,每一行数字组成的数(如第三行为)都是上一行的数与11的积.
(2)115=(10+1)5=105+5×104×1+10×103×1...
(1)11 (2)161051 (3)9;214358881
【解析】试题分析:观察图表寻找规律:三角形是一个有数字排列形成的三角形数表,它的两条斜边都是数字1组成,而其余的数则是等于它“肩”上的两个数之和.
试题解析:
(1)从第二行到第五行,每一行数字组成的数(如第三行为)都是上一行的数与11的积.
(2)115=(10+1)5=105+5×104×1+10×103×1... 
