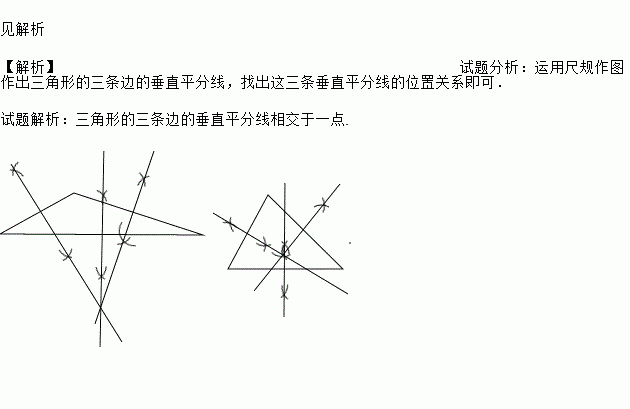
题目内容
利用尺规作三角形的三条边的垂直平分线,观察这三条垂直平分线的位置关系,你发现了什么?再换一个三角形试一试.
 见解析
【解析】试题分析:运用尺规作图作出三角形的三条边的垂直平分线,找出这三条垂直平分线的位置关系即可.
试题解析:三角形的三条边的垂直平分线相交于一点.
见解析
【解析】试题分析:运用尺规作图作出三角形的三条边的垂直平分线,找出这三条垂直平分线的位置关系即可.
试题解析:三角形的三条边的垂直平分线相交于一点.
下列图形中,右边图形与左边图形成轴对称的是(____)
A. 
B. 
C. 
D. 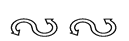
 B
【解析】A、是平移,不符合题意;B、是轴对称,符合题意;C、是旋转,不是轴对称,不符合题意;D、是平移,不符合题意,
故选B.
B
【解析】A、是平移,不符合题意;B、是轴对称,符合题意;C、是旋转,不是轴对称,不符合题意;D、是平移,不符合题意,
故选B. 如图,下列说法错误的是( )
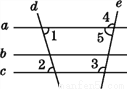
A. 若a∥b,b∥c,则a∥c B. 若∠1=∠2,则a∥c
C. 若∠3=∠2,则b∥c D. 若∠3+∠5=180°,则a∥c
 C
【解析】试题分析:根据平行线的判定进行判断即可.
【解析】
A、若a∥b,b∥c,则a∥c,利用了平行公理,正确;
B、若∠1=∠2,则a∥c,利用了内错角相等,两直线平行,正确;
C、∠3=∠2,不能判断b∥c,错误;
D、若∠3+∠5=180°,则a∥c,利用同旁内角互补,两直线平行,正确;
故选C.
C
【解析】试题分析:根据平行线的判定进行判断即可.
【解析】
A、若a∥b,b∥c,则a∥c,利用了平行公理,正确;
B、若∠1=∠2,则a∥c,利用了内错角相等,两直线平行,正确;
C、∠3=∠2,不能判断b∥c,错误;
D、若∠3+∠5=180°,则a∥c,利用同旁内角互补,两直线平行,正确;
故选C. 如图,∠1和∠2是直线_______和直线________被直线______所截得的同位角;
∠1和∠3是直线_______和直线________被直线______所截得的__________角;
∠2和∠4是直线_______和直线________被直线______所截得的__________角;
∠3和∠4是直线_______和直线________被直线______所截得的__________角;
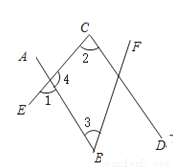
 AB,CD,CE;CE,BF,AB,内错;AB,CD,CE,同旁内;CE,BF,AB,同旁内
【解析】如图,∠1和∠2是直线AB和直线CD被直线CE所截得的同位角;
∠1和∠3是直线CE和直线BF被直线AB所截得的内错角;
∠2和∠4是直线AB和直线CD被直线CE所截得的同旁内角;
∠3和∠4是直线CE和直线BF被直线AB所截得的同旁内角;
AB,CD,CE;CE,BF,AB,内错;AB,CD,CE,同旁内;CE,BF,AB,同旁内
【解析】如图,∠1和∠2是直线AB和直线CD被直线CE所截得的同位角;
∠1和∠3是直线CE和直线BF被直线AB所截得的内错角;
∠2和∠4是直线AB和直线CD被直线CE所截得的同旁内角;
∠3和∠4是直线CE和直线BF被直线AB所截得的同旁内角; 如图,下列说法正确的是 ( )
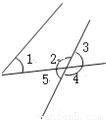
A. ∠1和∠2是内错角 B. ∠1和∠3是内错角
C. ∠1和∠4是内错角 D. ∠1和∠5是内错角
 D
【解析】A. ∵∠1和∠2是同旁内角,故不正确;
B. ∵∠1和∠3是同位角,故不正确;
C. ∵ ∠1和∠4不具备特殊位置关系,故不正确;
D. ∵∠1和∠5是内错角,故正确;
故选D.
D
【解析】A. ∵∠1和∠2是同旁内角,故不正确;
B. ∵∠1和∠3是同位角,故不正确;
C. ∵ ∠1和∠4不具备特殊位置关系,故不正确;
D. ∵∠1和∠5是内错角,故正确;
故选D. 到三角形三个顶点的距离都相等的点是这个三角形的( )
A. 三条高的交点 B. 三条角平分线的交点
C. 三条中线的交点 D. 三条边的垂直平分线的交点
 D
【解析】【解析】
到三角形三个顶点的距离都相等的点是这个三角形的三条边的垂直平分线的交点,故选D.
D
【解析】【解析】
到三角形三个顶点的距离都相等的点是这个三角形的三条边的垂直平分线的交点,故选D. 杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下:
如图,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD相交于O,OD⊥CD,垂足为D,已知AB=20米,请根据上述信息求标语CD的长度.
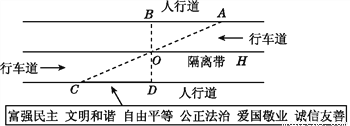
 20米.
【解析】试题分析:已知AB∥CD,根据平行线的性质可得∠ABO=∠CDO,再由垂直的定义可得∠CDO=90°,可得OB⊥AB,根据相邻两平行线间的距离相等可得OD=OB,即可根据ASA定理判定△ABO≌△CDO,由全等三角形的性质即可得CD=AB=20m.
试题解析:∵AB∥CD,∴∠ABO=∠CDO,
∵OD⊥CD,∴∠CDO=90°,
∴∠ABO=90°,即O...
20米.
【解析】试题分析:已知AB∥CD,根据平行线的性质可得∠ABO=∠CDO,再由垂直的定义可得∠CDO=90°,可得OB⊥AB,根据相邻两平行线间的距离相等可得OD=OB,即可根据ASA定理判定△ABO≌△CDO,由全等三角形的性质即可得CD=AB=20m.
试题解析:∵AB∥CD,∴∠ABO=∠CDO,
∵OD⊥CD,∴∠CDO=90°,
∴∠ABO=90°,即O... 如图,木工师傅在做完门框后,为防止变形常常象图中所示那样钉上两条斜拉的木条(图中的AB,CD两根木条),这样做是运用了三角形的( )
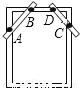
A. 全等性 B. 灵活性 C. 稳定性 D. 对称性
 C
【解析】三角形具有稳定性,其他多边形不具有稳定性,把多边形分割成三角形则多边形的形状就不会改变,故这样做是运用了三角形的稳定性.
故选:C.
C
【解析】三角形具有稳定性,其他多边形不具有稳定性,把多边形分割成三角形则多边形的形状就不会改变,故这样做是运用了三角形的稳定性.
故选:C. 若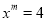 ,
, 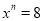 ,求
,求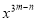 的值。
的值。
 8
【解析】试题分析:根据已知条件,逆用同底数幂的除法法则计算即可.
试题解析:
∵, ,
∴
8
【解析】试题分析:根据已知条件,逆用同底数幂的除法法则计算即可.
试题解析:
∵, ,
∴