题目内容
在△ABC中,AB=AC,BC=12,∠B=30°,AB的垂直平分线DE交BC边于点E,AC的垂直平分线MN交BC于点N.
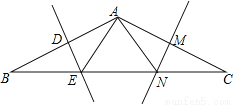
(1)求△AEN的周长;
(2)求证:BE=EN=NC.
 (1)12;(2)见解析
【解析】试题分析:(1)根据线段的垂直平分线的性质得到EB=EA,NA=NC,根据三角形的周长公式计算即可;
(2)根据等腰三角形的性质和三角形的外角的性质证明△AEN是等边三角形,等量代换证明即可.
试题解析:(1)∵DE是AB的垂直平分线,
∴EB=EA,
∵MN是AC的垂直平分线,
∴NA=NC,
则△AEN的周长=AE+A...
(1)12;(2)见解析
【解析】试题分析:(1)根据线段的垂直平分线的性质得到EB=EA,NA=NC,根据三角形的周长公式计算即可;
(2)根据等腰三角形的性质和三角形的外角的性质证明△AEN是等边三角形,等量代换证明即可.
试题解析:(1)∵DE是AB的垂直平分线,
∴EB=EA,
∵MN是AC的垂直平分线,
∴NA=NC,
则△AEN的周长=AE+A...
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案如图,在由四个小正方形组成的田字格中,△ABC的顶点都是小正方形的顶点.在田字格上画与△ABC成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形共有______________个.

 3
【解析】如图所示:符合题意的有3个三角形,
故答案为:3.
3
【解析】如图所示:符合题意的有3个三角形,
故答案为:3. 如图,下列推理正确的有( )
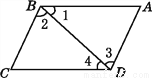
①因为∠1=∠4,所以BC∥AD;
②因为∠2=∠3,所以AB∥CD;
③因为∠BCD+∠ADC=180°,所以AD∥BC;
④因为∠1+∠2+∠C=180°,所以BC∥AD.
A. 1个 B. 2个 C. 3个 D. 4个
 A
【解析】(1)由∠1=∠2不能推导出BC∥AD,所以①中的推理错误;
(2)由∠2=∠3不能推导出AB∥CD,所以②中的推理错误;
(3)由∠BCD+∠ADC=180°能推导出BC∥AD,所以③中推理正确;
(4)由∠BCD+∠ABC=180°不能推导出BC∥AD,所以④中推理错误;
即4个推理中,只有③正确.
故选A.
A
【解析】(1)由∠1=∠2不能推导出BC∥AD,所以①中的推理错误;
(2)由∠2=∠3不能推导出AB∥CD,所以②中的推理错误;
(3)由∠BCD+∠ADC=180°能推导出BC∥AD,所以③中推理正确;
(4)由∠BCD+∠ABC=180°不能推导出BC∥AD,所以④中推理错误;
即4个推理中,只有③正确.
故选A. 如图,(1)如果∠1=__________,那么DE∥AC;(同位角相等,两直线平行);
(2)如果∠1=__________,那么EF∥BC;(内错角相等,两直线平行);
(3)如果∠DEF+__________=180°,那么DE∥AC;(同旁内角互补,两直线平行);
(4)如果∠2+__________=180°,那么AB∥DF;(同旁内角互补,两直线平行).
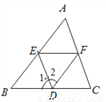
 ∠C; ∠DEF; ∠EFC; ∠AED.
【解析】(1)如果∠1=∠C ,那么DE//AC;(同位角相等,两直线平行)
(2)如果∠1=∠DEF ,那么EF//BC;(内错角相等,两直线平行)
(3)如果∠DEF+∠EFC =180°,那么DE//AC;(同旁内角互补,两直线平行)
(4)如果∠2+∠AED =180°,,那么AB//DF;(同旁内角互补,两直线平行)
...
∠C; ∠DEF; ∠EFC; ∠AED.
【解析】(1)如果∠1=∠C ,那么DE//AC;(同位角相等,两直线平行)
(2)如果∠1=∠DEF ,那么EF//BC;(内错角相等,两直线平行)
(3)如果∠DEF+∠EFC =180°,那么DE//AC;(同旁内角互补,两直线平行)
(4)如果∠2+∠AED =180°,,那么AB//DF;(同旁内角互补,两直线平行)
... 如图,点E在BC的延长线上,下列条件中能判定BC//AD的是 ( )
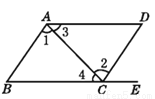
A. ∠1=∠2 B. ∠DAB+∠D=180° C. ∠3=∠4 D. ∠B=∠DCE
 C
【解析】A. ∵∠1=∠2 ,∴AB∥CD, 故不正确;
B. ∵ ∠DAB+∠D=180° ,∴AB∥CD, 故不正确;
C. ∵∠3=∠4 ,∴ BC∥AD, 故正确;
D. ∵∠B=∠DCE,∴AB∥CD, 故不正确;
故选C.
C
【解析】A. ∵∠1=∠2 ,∴AB∥CD, 故不正确;
B. ∵ ∠DAB+∠D=180° ,∴AB∥CD, 故不正确;
C. ∵∠3=∠4 ,∴ BC∥AD, 故正确;
D. ∵∠B=∠DCE,∴AB∥CD, 故不正确;
故选C. 如图,在△ABC中,DE是边AB的垂直平分线,BC=8cm,AC=5cm,则△ADC的周长为( )
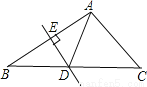
A. 14cm B. 13cm C. 11cm D. 9cm
 B
【解析】试题解析:∵DE是边AB的垂直平分线
∴BD=AD
∴△ADC的周长为AC+DC+AD=AC+BC=5+8=13cm.
故选B.
B
【解析】试题解析:∵DE是边AB的垂直平分线
∴BD=AD
∴△ADC的周长为AC+DC+AD=AC+BC=5+8=13cm.
故选B. 如图,已知零件的外径为a,要求它的厚度x,动手制作一个简单的工具,利用三角形全等的知识,求出x.
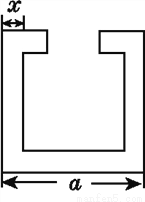
 .
【解析】试题分析:可设计如图所示的工具,利用△AOB≌△COD即可求解.
试题解析:可设计如图所示的工具,其中O为AC,BD的中点.
在△AOB和△COD中,
所以△AOB≌△COD(SAS).
所以AB=CD.所以测量出C,D之间的距离,CD的长就是A,B间的距离.
因为AB=a-2x,所以x==.
.
【解析】试题分析:可设计如图所示的工具,利用△AOB≌△COD即可求解.
试题解析:可设计如图所示的工具,其中O为AC,BD的中点.
在△AOB和△COD中,
所以△AOB≌△COD(SAS).
所以AB=CD.所以测量出C,D之间的距离,CD的长就是A,B间的距离.
因为AB=a-2x,所以x==. 如图,AB=CD,AD=CB,那么下列结论中错误的是( )
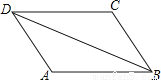
A. ∠A=∠C B. AB=AD C. AD∥BC D. AB∥CD
 B
【解析】∵在△ABD和△CDB中,
,
∴△ABD≌△CDB,
∴∠ADB=∠CBD,∠ABD=∠CDB,∠A=∠C
∴AD∥BC,AB∥CD,
∴A、C、D选项正确.
故选:B.
B
【解析】∵在△ABD和△CDB中,
,
∴△ABD≌△CDB,
∴∠ADB=∠CBD,∠ABD=∠CDB,∠A=∠C
∴AD∥BC,AB∥CD,
∴A、C、D选项正确.
故选:B. 已知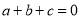 ,
, 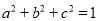 .
.
(1)求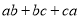 的值;
的值;
(2)求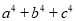 的值.
的值.
 (1) (2)
【解析】试题分析:(1)把a+b+c=0两边平方,然后利用代入法等量代换即可;
(2)把ab+bc+ca与两边分别乘方即可.
试题解析:(1)因为a+b+c=0
所以+2ab+2ac+2bc=0
∴2ab+2ac+2bc=-1
即ab+bc+ca=-
(2)因为a+b+c=0,a2+b2+c2=1
所以+2ab+2ac+2bc=0
...
(1) (2)
【解析】试题分析:(1)把a+b+c=0两边平方,然后利用代入法等量代换即可;
(2)把ab+bc+ca与两边分别乘方即可.
试题解析:(1)因为a+b+c=0
所以+2ab+2ac+2bc=0
∴2ab+2ac+2bc=-1
即ab+bc+ca=-
(2)因为a+b+c=0,a2+b2+c2=1
所以+2ab+2ac+2bc=0
... 
