7.某公司生产一种新型节能电水壶并加以销售,现准备在甲城市和乙城市两个不同地方按不同销售方案进行销售,以便开拓市场.
若只在甲城市销售,销售价格为y(元/件)、月销量为x(件),y是x的一次函数,如表,
成本为50元/件,无论销售多少,每月还需支出广告费72500元,设月利润为W甲(元)
(利润=销售额-成本-广告费).
若只在乙城市销售,销售价格为200元/件,受各种不确定因素影响,成本为a元/件(a为常数,40≤a≤70),当月销量为x(件)时,每月还需缴纳$\frac{1}{100}$x2元的附加费,设月利润为W乙(元)(利润=销售额-成本-附加费).
(1)当x=1000时,y甲=190元/件,w甲=67500元;
(2)分别求出W甲,W乙与x间的函数关系式(不必写x的取值范围);
(3)当x为何值时,在甲城市销售的月利润最大?若在乙城市销售月利润的最大值与在甲城市销售月利润的最大值相同,求a的值;
(4)如果某月要将5000件产品全部销售完,请你通过分析帮公司决策,选择在甲城市还是在乙城市销售才能使所获月利润较大?
若只在甲城市销售,销售价格为y(元/件)、月销量为x(件),y是x的一次函数,如表,
| 月销量x(件) | 1500 | 2000 |
| 销售价格y(元/件) | 185 | 180 |
(利润=销售额-成本-广告费).
若只在乙城市销售,销售价格为200元/件,受各种不确定因素影响,成本为a元/件(a为常数,40≤a≤70),当月销量为x(件)时,每月还需缴纳$\frac{1}{100}$x2元的附加费,设月利润为W乙(元)(利润=销售额-成本-附加费).
(1)当x=1000时,y甲=190元/件,w甲=67500元;
(2)分别求出W甲,W乙与x间的函数关系式(不必写x的取值范围);
(3)当x为何值时,在甲城市销售的月利润最大?若在乙城市销售月利润的最大值与在甲城市销售月利润的最大值相同,求a的值;
(4)如果某月要将5000件产品全部销售完,请你通过分析帮公司决策,选择在甲城市还是在乙城市销售才能使所获月利润较大?
3.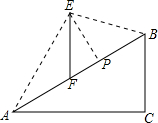 如图,在坡度i=1:$\sqrt{3}$的斜坡AB上立有一电线杆EF,工程师在点A处测得E的仰角为60°,沿斜坡前进20米到达B,此时测得点E的仰角为15°,现要在斜坡AB上找一点P,在P处安装一根拉绳PE来固定电线杆,以使EF保持竖直,为使拉绳PE最短,则FP的长度约为( )(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,在坡度i=1:$\sqrt{3}$的斜坡AB上立有一电线杆EF,工程师在点A处测得E的仰角为60°,沿斜坡前进20米到达B,此时测得点E的仰角为15°,现要在斜坡AB上找一点P,在P处安装一根拉绳PE来固定电线杆,以使EF保持竖直,为使拉绳PE最短,则FP的长度约为( )(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
 如图,在坡度i=1:$\sqrt{3}$的斜坡AB上立有一电线杆EF,工程师在点A处测得E的仰角为60°,沿斜坡前进20米到达B,此时测得点E的仰角为15°,现要在斜坡AB上找一点P,在P处安装一根拉绳PE来固定电线杆,以使EF保持竖直,为使拉绳PE最短,则FP的长度约为( )(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,在坡度i=1:$\sqrt{3}$的斜坡AB上立有一电线杆EF,工程师在点A处测得E的仰角为60°,沿斜坡前进20米到达B,此时测得点E的仰角为15°,现要在斜坡AB上找一点P,在P处安装一根拉绳PE来固定电线杆,以使EF保持竖直,为使拉绳PE最短,则FP的长度约为( )(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)| A. | 3.7米 | B. | 3.9米 | C. | 4.2米 | D. | 5.7米 |
2. 某电信公司提供的移动通讯服务的收费标准有两种套餐如表:
某电信公司提供的移动通讯服务的收费标准有两种套餐如表:
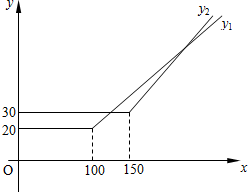
设每月通话时间为x分种,A,B两种套餐每月话费分别为y1,y2元.y1,y2关于x的函数图象如图所示.
(1)表格中的a=20,b=150;
(2)通话时间超过每月免费通话时间后,求y1,y2关于x的函数关系式,并写出相应的取值范围;
(3)已知甲乙两人分别使用A,B两种套餐,他们的通话时间都是t分钟(t>150),但话费相差5元,求两人的通话时间.
 某电信公司提供的移动通讯服务的收费标准有两种套餐如表:
某电信公司提供的移动通讯服务的收费标准有两种套餐如表:| A套餐 | B套餐 | |
| 每月基本服务费 | a | 30 |
| 每月免费通话时间 | 100 | b |
| 超出每分钟收费 | 0.4 | 0.5 |
(1)表格中的a=20,b=150;
(2)通话时间超过每月免费通话时间后,求y1,y2关于x的函数关系式,并写出相应的取值范围;
(3)已知甲乙两人分别使用A,B两种套餐,他们的通话时间都是t分钟(t>150),但话费相差5元,求两人的通话时间.
20.A、B两地相距60千米,甲、乙两人驾车(匀速)从A地驶向B,甲的时速为120千米,乙的时速为90千米,如果乙比甲早出发6分钟,则当甲追上乙以后,乙再过( )分钟可以到达B.
0 284353 284361 284367 284371 284377 284379 284383 284389 284391 284397 284403 284407 284409 284413 284419 284421 284427 284431 284433 284437 284439 284443 284445 284447 284448 284449 284451 284452 284453 284455 284457 284461 284463 284467 284469 284473 284479 284481 284487 284491 284493 284497 284503 284509 284511 284517 284521 284523 284529 284533 284539 284547 366461
| A. | 25 | B. | 20 | C. | 16 | D. | 10 |
