题目内容
3.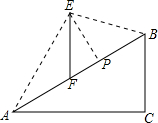 如图,在坡度i=1:$\sqrt{3}$的斜坡AB上立有一电线杆EF,工程师在点A处测得E的仰角为60°,沿斜坡前进20米到达B,此时测得点E的仰角为15°,现要在斜坡AB上找一点P,在P处安装一根拉绳PE来固定电线杆,以使EF保持竖直,为使拉绳PE最短,则FP的长度约为( )(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,在坡度i=1:$\sqrt{3}$的斜坡AB上立有一电线杆EF,工程师在点A处测得E的仰角为60°,沿斜坡前进20米到达B,此时测得点E的仰角为15°,现要在斜坡AB上找一点P,在P处安装一根拉绳PE来固定电线杆,以使EF保持竖直,为使拉绳PE最短,则FP的长度约为( )(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)| A. | 3.7米 | B. | 3.9米 | C. | 4.2米 | D. | 5.7米 |
分析 要使点E到AB的距离最短,则EP⊥AB,根据题目中的信息可以求得FP的长度,本题得以解决.
解答 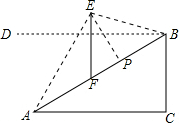 解:作BD∥AC,如右图所示,
解:作BD∥AC,如右图所示,
∵斜坡AB的坡度i=1:$\sqrt{3}$,
∴tan∠BAC=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠BAC=30°,
∵∠EAC=60°,
∴∠EAF=30°,
∵要使点E到AB的距离最短,
∴EP⊥AB于点P,
∴tan∠EAP=$\frac{EP}{AP}$,
∴AP=$\frac{EP}{tan30°}$,
∵∠EBD=15°,BD∥AC,
∴∠DBA=∠BAC=30°,
∴∠EBP=45°,
∴EP=PB,
∵AP+PB=AB=20米,
∴$\frac{EP}{tan30°}$+EP=20,
解得,EP=10$\sqrt{3}$-10,
又∵EF∥BC,∠B=90°-∠BAC=60°,
∴∠EFP=60°,
∵tan∠EFP=$\frac{EP}{PF}$,
即tan60°=$\frac{10\sqrt{3}-10}{PF}$,
解得,PF≈4.2米,
故选C.
点评 本题考查解直角三角形的应用-坡度坡角问题、仰角俯角问题,解题的关键是明确题意,找出所求问题需要的条件,利用特殊角的三角函数进行解答,注意挖掘题目中的隐含条件.

练习册系列答案
相关题目
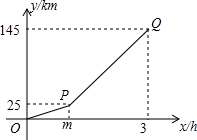 甲、乙两地相距145km,小李骑摩托车从甲地出发去往乙地,速度为25km/h,中途因故换成汽车继续前往乙地(换车时间忽略不计),小李与甲地的距离y(单位:km)和所用时间x(单位:h)之间的关系如图所示.
甲、乙两地相距145km,小李骑摩托车从甲地出发去往乙地,速度为25km/h,中途因故换成汽车继续前往乙地(换车时间忽略不计),小李与甲地的距离y(单位:km)和所用时间x(单位:h)之间的关系如图所示. 如图,秋千链子的长度OA=3m,静止时秋千踏板处于A位置.此时踏板距离地面0.3m,秋千向两边摆动.当踏板处于A′位置时,摆角最大,即∠AOA′=50°,则在A′位置,踏板与地面的距离为1.37m.(sin50°≈0.766,cos50°≈0.6428,结果精确到0.01m)
如图,秋千链子的长度OA=3m,静止时秋千踏板处于A位置.此时踏板距离地面0.3m,秋千向两边摆动.当踏板处于A′位置时,摆角最大,即∠AOA′=50°,则在A′位置,踏板与地面的距离为1.37m.(sin50°≈0.766,cos50°≈0.6428,结果精确到0.01m)