12. 如图,在Rt△ABC中,∠C=90°,AC=4,BC=7,点D在边BC上,CD=3,⊙A的半径长为3,⊙D与⊙A相交,且点B在⊙D外,那么⊙D的半径长r的取值范围是( )
如图,在Rt△ABC中,∠C=90°,AC=4,BC=7,点D在边BC上,CD=3,⊙A的半径长为3,⊙D与⊙A相交,且点B在⊙D外,那么⊙D的半径长r的取值范围是( )
 如图,在Rt△ABC中,∠C=90°,AC=4,BC=7,点D在边BC上,CD=3,⊙A的半径长为3,⊙D与⊙A相交,且点B在⊙D外,那么⊙D的半径长r的取值范围是( )
如图,在Rt△ABC中,∠C=90°,AC=4,BC=7,点D在边BC上,CD=3,⊙A的半径长为3,⊙D与⊙A相交,且点B在⊙D外,那么⊙D的半径长r的取值范围是( )| A. | 1<r<4 | B. | 2<r<4 | C. | 1<r<8 | D. | 2<r<8 |
11.已知在△ABC中,AB=AC,AD是角平分线,点D在边BC上,设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,那么向量$\overrightarrow{AC}$用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示为( )
| A. | $\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$ | C. | -$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$ | D. | -$\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$ |
8.已知反比例函数y=$\frac{6}{x}$,当1<x<3时,y的最小整数值是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
7.若点O是等腰△ABC的外心,且∠BOC=60°,底边BC=2,则△ABC的面积为( )
| A. | 2+$\sqrt{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | 2+$\sqrt{3}$或2-$\sqrt{3}$ | D. | 4+2$\sqrt{3}$或2-$\sqrt{3}$ |
6.如图,直角边长为1的等腰直角三角形与边长为2的正方形在同一水平线上,三角形沿水平线从左向右匀速穿过正方形.设穿过时间为t,正方形与三角形不重合部分的面积为s(阴影部分),则s与t的大致图象为( )


| A. | 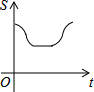 | B. | 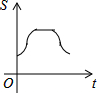 | C. | 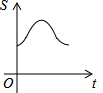 | D. |  |
3.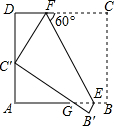 如图,正方形ABCD的边长为3,E、F分别是AB、CD上的点,且∠CFE=60°,将四边形BCFE沿EF翻折,得到B′C′FE,C′恰好落在AD边上,B′C′交AB于点G,则GE的长是( )
如图,正方形ABCD的边长为3,E、F分别是AB、CD上的点,且∠CFE=60°,将四边形BCFE沿EF翻折,得到B′C′FE,C′恰好落在AD边上,B′C′交AB于点G,则GE的长是( )
0 284218 284226 284232 284236 284242 284244 284248 284254 284256 284262 284268 284272 284274 284278 284284 284286 284292 284296 284298 284302 284304 284308 284310 284312 284313 284314 284316 284317 284318 284320 284322 284326 284328 284332 284334 284338 284344 284346 284352 284356 284358 284362 284368 284374 284376 284382 284386 284388 284394 284398 284404 284412 366461
 如图,正方形ABCD的边长为3,E、F分别是AB、CD上的点,且∠CFE=60°,将四边形BCFE沿EF翻折,得到B′C′FE,C′恰好落在AD边上,B′C′交AB于点G,则GE的长是( )
如图,正方形ABCD的边长为3,E、F分别是AB、CD上的点,且∠CFE=60°,将四边形BCFE沿EF翻折,得到B′C′FE,C′恰好落在AD边上,B′C′交AB于点G,则GE的长是( )| A. | 3$\sqrt{3}$-4 | B. | 4$\sqrt{2}$-5 | C. | 4-2$\sqrt{3}$ | D. | 5-2$\sqrt{3}$ |
 如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论正确的个数是( )
如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论正确的个数是( )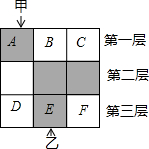 如图,3×3的方格分为上中下三层,第一层有一枚黑色方块甲,可在方格A、B、C中移动,第二层有两枚固定不动的黑色方块,第三层有一枚黑色方块乙,可在方格D、E、F中移动,甲、乙移入方格后,四枚黑色方块构成各种拼图.
如图,3×3的方格分为上中下三层,第一层有一枚黑色方块甲,可在方格A、B、C中移动,第二层有两枚固定不动的黑色方块,第三层有一枚黑色方块乙,可在方格D、E、F中移动,甲、乙移入方格后,四枚黑色方块构成各种拼图.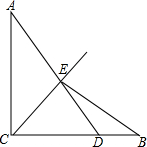 如图,AC⊥BC,AC=BC,D是BC上一点,连接AD,与∠ACB的平分线交于点E,连接BE.若S△ACE=$\frac{6}{7}$,S△BDE=$\frac{3}{14}$,则AC=2.
如图,AC⊥BC,AC=BC,D是BC上一点,连接AD,与∠ACB的平分线交于点E,连接BE.若S△ACE=$\frac{6}{7}$,S△BDE=$\frac{3}{14}$,则AC=2.