题目内容
8.已知反比例函数y=$\frac{6}{x}$,当1<x<3时,y的最小整数值是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 根据反比例函数系数k>0,结合反比例函数的性质即可得知该反比例函数在x>0中单调递减,再结合x的取值范围,可得出y的取值范围,取其内的最小整数,本题得解.
解答 解:在反比例函数y=$\frac{6}{x}$中k=6>0,
∴该反比例函数在x>0内,y随x的增大而减小,
当x=3时,y=$\frac{6}{3}$=2;当x=1时,y=$\frac{6}{1}$=6.
∴当1<x<3时,2<y<6.
∴y的最小整数值是3.
故选A.
点评 本题考查了反比例函数的性质,解题的关键是找出反比例函数y=$\frac{6}{x}$在1<x<3中y的取值范围.本题属于基础题,难度不大,解决该题型题目时,根据反比例函数的系数结合反比例函数的性质得出该反比例函数的单调性是关键.

练习册系列答案
相关题目
18.下列二次根式中的最简二次根式是( )
| A. | $\sqrt{9}$ | B. | $\sqrt{24}$ | C. | $\sqrt{30}$ | D. | $\sqrt{\frac{2}{3}}$ |
19.若二次函数y=x2+mx的对称轴是x=3,则关于x的方程x2+mx=7的解为( )
| A. | x1=0,x2=6 | B. | x1=1,x2=7 | C. | x1=1,x2=-7 | D. | x1=-1,x2=7 |
3.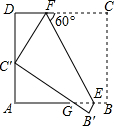 如图,正方形ABCD的边长为3,E、F分别是AB、CD上的点,且∠CFE=60°,将四边形BCFE沿EF翻折,得到B′C′FE,C′恰好落在AD边上,B′C′交AB于点G,则GE的长是( )
如图,正方形ABCD的边长为3,E、F分别是AB、CD上的点,且∠CFE=60°,将四边形BCFE沿EF翻折,得到B′C′FE,C′恰好落在AD边上,B′C′交AB于点G,则GE的长是( )
 如图,正方形ABCD的边长为3,E、F分别是AB、CD上的点,且∠CFE=60°,将四边形BCFE沿EF翻折,得到B′C′FE,C′恰好落在AD边上,B′C′交AB于点G,则GE的长是( )
如图,正方形ABCD的边长为3,E、F分别是AB、CD上的点,且∠CFE=60°,将四边形BCFE沿EF翻折,得到B′C′FE,C′恰好落在AD边上,B′C′交AB于点G,则GE的长是( )| A. | 3$\sqrt{3}$-4 | B. | 4$\sqrt{2}$-5 | C. | 4-2$\sqrt{3}$ | D. | 5-2$\sqrt{3}$ |
18.已知一组数据:3,4,6,7,8,8,下列说法正确的是( )
| A. | 众数是2 | B. | 众数是8 | C. | 中位数是6 | D. | 中位数是7 |
 如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F. 如图所示,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象经过矩形OABC的对角线AC的中点D.若矩形OABC的面积为8,则k的值为2.
如图所示,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象经过矩形OABC的对角线AC的中点D.若矩形OABC的面积为8,则k的值为2.