题目内容
11.已知在△ABC中,AB=AC,AD是角平分线,点D在边BC上,设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,那么向量$\overrightarrow{AC}$用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示为( )| A. | $\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$ | C. | -$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$ | D. | -$\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$ |
分析 由△ABC中,AD是角平分线,结合等腰三角形的性质得出BD=DC,可求得$\overrightarrow{DC}$的值,然后利用三角形法则,求得答案.
解答  解:如图所示:∵在△ABC中,AB=AC,AD是角平分线,
解:如图所示:∵在△ABC中,AB=AC,AD是角平分线,
∴BD=DC,
∵$\overrightarrow{BC}$=$\overrightarrow{a}$,
∴$\overrightarrow{DC}$=$\frac{1}{2}$$\overrightarrow{a}$,
∵$\overrightarrow{AD}$=$\overrightarrow{b}$,
∴$\overrightarrow{AC}$=$\overrightarrow{AD}$+$\overrightarrow{DC}$=$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$.
故选:A.
点评 此题考查了平面向量的知识,注意掌握三角形法则的应用是解题关键.

练习册系列答案
相关题目
1. 如图,在矩形ABCD中,对角线AC、BD交于点O,以下结论错误的是( )
如图,在矩形ABCD中,对角线AC、BD交于点O,以下结论错误的是( )
 如图,在矩形ABCD中,对角线AC、BD交于点O,以下结论错误的是( )
如图,在矩形ABCD中,对角线AC、BD交于点O,以下结论错误的是( )| A. | ∠ABC=90° | B. | △OAD是等边三角形 | ||
| C. | OA=OB;OC=OB | D. | AC=BD |
6.如图,直角边长为1的等腰直角三角形与边长为2的正方形在同一水平线上,三角形沿水平线从左向右匀速穿过正方形.设穿过时间为t,正方形与三角形不重合部分的面积为s(阴影部分),则s与t的大致图象为( )


| A. |  | B. |  | C. |  | D. |  |
3.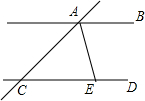 如图,直线AB∥CD,AE平分∠CAB.AE与CD相交于点E,∠ACD=40°,则∠BAE的度数是( )
如图,直线AB∥CD,AE平分∠CAB.AE与CD相交于点E,∠ACD=40°,则∠BAE的度数是( )
 如图,直线AB∥CD,AE平分∠CAB.AE与CD相交于点E,∠ACD=40°,则∠BAE的度数是( )
如图,直线AB∥CD,AE平分∠CAB.AE与CD相交于点E,∠ACD=40°,则∠BAE的度数是( )| A. | 40° | B. | 70° | C. | 80° | D. | 140° |
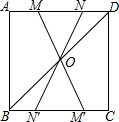 如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )
如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( ) 如图,将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开,得到△ACD,再将△ACD沿DB方向平移到△A′C′D′的位置,若平移开始后点D′未到达点B时,A′C′交CD于E,D′C′交CB于点F,连接EF,当四边形EDD′F为菱形时,试探究△A′DE的形状,并判断△A′DE与△EFC′是否全等?请说明理由.
如图,将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开,得到△ACD,再将△ACD沿DB方向平移到△A′C′D′的位置,若平移开始后点D′未到达点B时,A′C′交CD于E,D′C′交CB于点F,连接EF,当四边形EDD′F为菱形时,试探究△A′DE的形状,并判断△A′DE与△EFC′是否全等?请说明理由.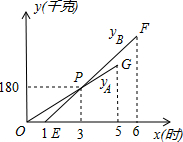 某物流公司引进A、B两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时,A种机器人于某日0时开始搬运,过了1小时,B种机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(千克)与时间x(时)的函数图象,线段EF表示B种机器人的搬运量yB(千克)与时间x(时)的函数图象.根据图象提供的信息,解答下列问题:
某物流公司引进A、B两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时,A种机器人于某日0时开始搬运,过了1小时,B种机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(千克)与时间x(时)的函数图象,线段EF表示B种机器人的搬运量yB(千克)与时间x(时)的函数图象.根据图象提供的信息,解答下列问题: