题目内容
9. 如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论正确的个数是( )
如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论正确的个数是( )①AE=BF;②AE⊥BF;③sin∠BQP=$\frac{4}{5}$;④S四边形ECFG=2S△BGE.
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 首先证明△ABE≌△BCF,再利用角的关系求得∠BGE=90°,即可得到①AE=BF;②AE⊥BF;△BCF沿BF对折,得到△BPF,利用角的关系求出QF=QB,解出BP,QB,根据正弦的定义即可求解;根据AA可证△BGE与△BCF相似,进一步得到相似比,再根据相似三角形的性质即可求解.
解答 解:∵E,F分别是正方形ABCD边BC,CD的中点,
∴CF=BE,
在△ABE和△BCF中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABE=∠BCF}\\{BE=CF}\end{array}\right.$,
∴Rt△ABE≌Rt△BCF(SAS),
∴∠BAE=∠CBF,AE=BF,故①正确;
又∵∠BAE+∠BEA=90°,
∴∠CBF+∠BEA=90°,
∴∠BGE=90°,
∴AE⊥BF,故②正确;
根据题意得,FP=FC,∠PFB=∠BFC,∠FPB=90°
∵CD∥AB,
∴∠CFB=∠ABF,
∴∠ABF=∠PFB,
∴QF=QB,
令PF=k(k>0),则PB=2k
在Rt△BPQ中,设QB=x,
∴x2=(x-k)2+4k2,
∴x=$\frac{5k}{2}$,
∴sin=∠BQP=$\frac{BP}{QB}$=$\frac{4}{5}$,故③正确;
∵∠BGE=∠BCF,∠GBE=∠CBF,
∴△BGE∽△BCF,
∵BE=$\frac{1}{2}$BC,BF=$\frac{\sqrt{5}}{2}$BC,
∴BE:BF=1:$\sqrt{5}$,
∴△BGE的面积:△BCF的面积=1:5,
∴S四边形ECFG=4S△BGE,故④错误.
故选:B.
点评 本题主要考查了四边形的综合题,涉及正方形的性质、全等三角形的判定和性质、相似三角形的判定和性质以及折叠的性质的知识点,解决的关键是明确三角形翻转后边的大小不变,找准对应边,角的关系求解.

| A. | $\sqrt{8}$ | B. | $\sqrt{3}$ | C. | $\sqrt{12}$ | D. | $\sqrt{6}$ |
 秋季新学期开学时,红城中学对七年级新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格,现学校随机选取了部分学生的成绩,整理并制作成了如下不完整的图表:
秋季新学期开学时,红城中学对七年级新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格,现学校随机选取了部分学生的成绩,整理并制作成了如下不完整的图表:| 分 数 段 | 频数 | 频率 |
| 60≤x<70 | 9 | a |
| 70≤x<80 | 36 | 0.4 |
| 80≤x<90 | 27 | b |
| 90≤x≤100 | c | 0.2 |
(1)在表中,a=0.1,b=0.3,c=18;
(2)补全频数直方图;
(3)根据以上选取的数据,计算七年级学生的平均成绩.
(4)如果测试成绩不低于80分者为“优秀”等次,请你估计全校七年级的800名学生中,“优秀”等次的学生约有多少人?
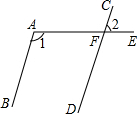 如图,AB∥CD,射线AE交CD于点F,若∠1=115°,则∠2的度数是( )
如图,AB∥CD,射线AE交CD于点F,若∠1=115°,则∠2的度数是( )| A. | 55° | B. | 65° | C. | 75° | D. | 85° |
| A. | x1=2,x2=-6 | B. | x1=-2,x2=6 | C. | x1=-2,x2=-6 | D. | x1=2,x2=6 |
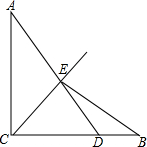 如图,AC⊥BC,AC=BC,D是BC上一点,连接AD,与∠ACB的平分线交于点E,连接BE.若S△ACE=$\frac{6}{7}$,S△BDE=$\frac{3}{14}$,则AC=2.
如图,AC⊥BC,AC=BC,D是BC上一点,连接AD,与∠ACB的平分线交于点E,连接BE.若S△ACE=$\frac{6}{7}$,S△BDE=$\frac{3}{14}$,则AC=2. 如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,-4)
如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,-4) 如图,⊙O的直径CD=20cm,AB是⊙O的弦,AB⊥CD,垂足为M,若OM=6cm,则AB的长为16cm.
如图,⊙O的直径CD=20cm,AB是⊙O的弦,AB⊥CD,垂足为M,若OM=6cm,则AB的长为16cm.