题目内容
3.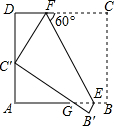 如图,正方形ABCD的边长为3,E、F分别是AB、CD上的点,且∠CFE=60°,将四边形BCFE沿EF翻折,得到B′C′FE,C′恰好落在AD边上,B′C′交AB于点G,则GE的长是( )
如图,正方形ABCD的边长为3,E、F分别是AB、CD上的点,且∠CFE=60°,将四边形BCFE沿EF翻折,得到B′C′FE,C′恰好落在AD边上,B′C′交AB于点G,则GE的长是( )| A. | 3$\sqrt{3}$-4 | B. | 4$\sqrt{2}$-5 | C. | 4-2$\sqrt{3}$ | D. | 5-2$\sqrt{3}$ |
分析 由正方形的性质得出∠A=∠B=∠C=∠D=90°,AB=AD=3,由折叠的性质得出FC′=FC,∠C′FE=∠CFE=60°,∠FC′B′=∠C=90°,B′E=BE,∠B′=∠B=90°,求出∠DC′F=30°,得出FC′=FC=2DF,求出DF=1,DC′=$\sqrt{3}$DF=$\sqrt{3}$,则C′A=3-$\sqrt{3}$,AG=$\sqrt{3}$(3-$\sqrt{3}$),设EB=x,则GE=2x,得出方程,解方程即可.
解答 解:∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=AD=3,
由折叠的性质得:FC′=FC,∠C′FE=∠CFE=60°,∠FC′B′=∠C=90°,B′E=BE,∠B′=∠B=90°,
∴∠DFC′=60°,
∴∠DC′F=30°,
∴FC′=FC=2DF,
∵DF+CF=CD=3,
∴DF+2DF=3,
解得:DF=1,
∴DC′=$\sqrt{3}$DF=$\sqrt{3}$,
则C′A=3-$\sqrt{3}$,AG=$\sqrt{3}$(3-$\sqrt{3}$),
设EB=x,
∵∠B′GE=∠AGC′=∠DC′F=30°,
∴GE=2x,
则$\sqrt{3}$(3-$\sqrt{3}$)+3x=3,
解得:x=2-$\sqrt{3}$,
∴GE=4-2$\sqrt{3}$;
故选:C.
点评 本题考查了翻折变换的性质、正方形的性质、勾股定理、含30°角的直角三角形的性质等知识;熟练掌握翻折变换和正方形的性质,根据题意得出方程是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13. 如图,将矩形ABCD沿EF折叠,使点B,D重合,已知AB=3,AD=4,则
如图,将矩形ABCD沿EF折叠,使点B,D重合,已知AB=3,AD=4,则
①DE=DF;②DF=EF;③△DCF≌△DGE;④EF=$\frac{15}{4}$.
上面结论正确的有( )
 如图,将矩形ABCD沿EF折叠,使点B,D重合,已知AB=3,AD=4,则
如图,将矩形ABCD沿EF折叠,使点B,D重合,已知AB=3,AD=4,则①DE=DF;②DF=EF;③△DCF≌△DGE;④EF=$\frac{15}{4}$.
上面结论正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.若代数式x+2的值为1,则x等于( )
| A. | 1 | B. | -1 | C. | 3 | D. | -3 |
18.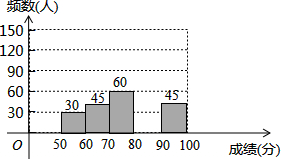 为了弘扬荆州优秀传统文化,某中学举办了荆州文化知识大赛,其规则是:每位参赛选手回答100道选择题,答对一题得1分,不答或错答不得分、不扣分,赛后对全体参赛选手的答题情况进行了相关统计,整理并绘制成如下图表:
为了弘扬荆州优秀传统文化,某中学举办了荆州文化知识大赛,其规则是:每位参赛选手回答100道选择题,答对一题得1分,不答或错答不得分、不扣分,赛后对全体参赛选手的答题情况进行了相关统计,整理并绘制成如下图表:
请根据以图表信息,解答下列问题:
(1)表中m=120,n=0.2;
(2)补全频数分布直方图;
(3)全体参赛选手成绩的中位数落在第几组;
(4)若得分在80分以上(含80分)的选手可获奖,记者从所有参赛选手中随机采访1人,求这名选手恰好是获奖者的概率.
 为了弘扬荆州优秀传统文化,某中学举办了荆州文化知识大赛,其规则是:每位参赛选手回答100道选择题,答对一题得1分,不答或错答不得分、不扣分,赛后对全体参赛选手的答题情况进行了相关统计,整理并绘制成如下图表:
为了弘扬荆州优秀传统文化,某中学举办了荆州文化知识大赛,其规则是:每位参赛选手回答100道选择题,答对一题得1分,不答或错答不得分、不扣分,赛后对全体参赛选手的答题情况进行了相关统计,整理并绘制成如下图表:| 组别 | 分数段 | 频数(人) | 频率 |
| 1 | 50≤x<60 | 30 | 0.1 |
| 2 | 60≤x<70 | 45 | 0.15 |
| 3 | 70≤x<80 | 60 | n |
| 4 | 80≤x<90 | m | 0.4 |
| 5 | 90≤x<100 | 45 | 0.15 |
(1)表中m=120,n=0.2;
(2)补全频数分布直方图;
(3)全体参赛选手成绩的中位数落在第几组;
(4)若得分在80分以上(含80分)的选手可获奖,记者从所有参赛选手中随机采访1人,求这名选手恰好是获奖者的概率.
8.已知反比例函数y=$\frac{6}{x}$,当1<x<3时,y的最小整数值是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
12.化简$\frac{{a}^{2}}{a-1}$-(a+1)的结果是( )
| A. | $\frac{1}{a-1}$ | B. | -$\frac{1}{a-1}$ | C. | $\frac{2a-1}{a-1}$ | D. | -$\frac{2a-1}{a-1}$ |
 如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(-2,0),且tan∠ACO=2.
如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(-2,0),且tan∠ACO=2.