题目内容
4.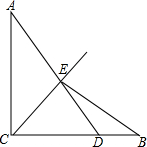 如图,AC⊥BC,AC=BC,D是BC上一点,连接AD,与∠ACB的平分线交于点E,连接BE.若S△ACE=$\frac{6}{7}$,S△BDE=$\frac{3}{14}$,则AC=2.
如图,AC⊥BC,AC=BC,D是BC上一点,连接AD,与∠ACB的平分线交于点E,连接BE.若S△ACE=$\frac{6}{7}$,S△BDE=$\frac{3}{14}$,则AC=2.
分析 设BC=4x,根据面积公式计算,得出BC=4BD,过E作AC,BC的垂线,垂足分别为F,G;证明CFEG为正方形,然后在直角三角形ACD中,利用三角形相似,求出正方形的边长(用x表示),再利用已知的面积建立等式,解出x,最后求出AC=BC=4x即可.
解答 解: 过E作AC,BC的垂线,垂足分别为F,G,
过E作AC,BC的垂线,垂足分别为F,G,
设BC=4x,则AC=4x,
∵CE是∠ACB的平分线,EF⊥AC,EG⊥BC,
∴EF=EG,又S△ACE=$\frac{6}{7}$,S△BDE=$\frac{3}{14}$,
∴BD=$\frac{1}{4}$AC=x,
∴CD=3x,
∵四边形EFCG是正方形,
∴EF=FC,
∵EF∥CD,
∴$\frac{EF}{CD}$=$\frac{AF}{AC}$,即$\frac{EF}{3x}$=$\frac{4x-EF}{4x}$,
解得,EF=$\frac{12}{7}$x,
则$\frac{1}{2}$×4x×$\frac{12}{7}$x=$\frac{6}{7}$,
解得,x=$\frac{1}{2}$,
则AC=4x=2,
故答案为:2.
点评 本题考查的是相似三角形的性质、角平分线的性质,掌握相似三角形的对应边的比相等、角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
相关题目
14. 如图,在周长为20cm的?ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为( )
如图,在周长为20cm的?ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为( )
 如图,在周长为20cm的?ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为( )
如图,在周长为20cm的?ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为( )| A. | 10cm | B. | 8cm | C. | 6cm | D. | 4cm |
12.下列运算正确的是( )
| A. | -2(a+b)=-2a+2b | B. | (a2)3=a5 | C. | a3+4a=$\frac{1}{4}$a3 | D. | 3a2•2a3=6a5 |
14.下列各数是无理数的是( )
| A. | 0 | B. | -1 | C. | $\sqrt{2}$ | D. | $\frac{3}{7}$ |
 如图,AB是⊙O的直径,AC、BC是⊙O的弦,直径DE⊥AC于点P.若点D在优弧$\widehat{ABC}$上,AB=8,BC=3,则DP=5.5.
如图,AB是⊙O的直径,AC、BC是⊙O的弦,直径DE⊥AC于点P.若点D在优弧$\widehat{ABC}$上,AB=8,BC=3,则DP=5.5. 如图,将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开,得到△ACD,再将△ACD沿DB方向平移到△A′C′D′的位置,若平移开始后点D′未到达点B时,A′C′交CD于E,D′C′交CB于点F,连接EF,当四边形EDD′F为菱形时,试探究△A′DE的形状,并判断△A′DE与△EFC′是否全等?请说明理由.
如图,将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开,得到△ACD,再将△ACD沿DB方向平移到△A′C′D′的位置,若平移开始后点D′未到达点B时,A′C′交CD于E,D′C′交CB于点F,连接EF,当四边形EDD′F为菱形时,试探究△A′DE的形状,并判断△A′DE与△EFC′是否全等?请说明理由. 如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论正确的个数是( )
如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论正确的个数是( )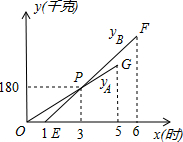 某物流公司引进A、B两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时,A种机器人于某日0时开始搬运,过了1小时,B种机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(千克)与时间x(时)的函数图象,线段EF表示B种机器人的搬运量yB(千克)与时间x(时)的函数图象.根据图象提供的信息,解答下列问题:
某物流公司引进A、B两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时,A种机器人于某日0时开始搬运,过了1小时,B种机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(千克)与时间x(时)的函数图象,线段EF表示B种机器人的搬运量yB(千克)与时间x(时)的函数图象.根据图象提供的信息,解答下列问题: 如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形OCED的周长为( )
如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形OCED的周长为( )