题目内容
12. 如图,在Rt△ABC中,∠C=90°,AC=4,BC=7,点D在边BC上,CD=3,⊙A的半径长为3,⊙D与⊙A相交,且点B在⊙D外,那么⊙D的半径长r的取值范围是( )
如图,在Rt△ABC中,∠C=90°,AC=4,BC=7,点D在边BC上,CD=3,⊙A的半径长为3,⊙D与⊙A相交,且点B在⊙D外,那么⊙D的半径长r的取值范围是( )| A. | 1<r<4 | B. | 2<r<4 | C. | 1<r<8 | D. | 2<r<8 |
分析 连接AD,
根据勾股定理得到AD=5,
根据圆与圆的位置关系得到r>5-3=2,
由点B在⊙D外,
于是得到r<4,
即可得到结论.
解答  解:连接AD,
解:连接AD,
∵AC=4,CD=3,∠C=90°,
∴AD=5,
∵⊙A的半径长为3,⊙D与⊙A相交,
∴r>5-3=2,
∵BC=7,
∴BD=4,
∵点B在⊙D外,
∴r<4,
∴⊙D的半径长r的取值范围是2<r<4,
故选B.
点评 本题考查了圆与圆的位置关系,点与圆的位置关系,设点到圆心的距离为d,则当d=r时,点在圆上;当d>r时,点在圆外;当d<r时,点在圆内.

练习册系列答案
相关题目
2.下列运算正确的是( )
| A. | 3$\sqrt{2}$-$\sqrt{2}$=3 | B. | 3$\sqrt{3}$×2$\sqrt{2}$=6$\sqrt{5}$ | C. | 3$\sqrt{5}$÷$\frac{1}{{\sqrt{3}}}$×$\sqrt{3}$=3$\sqrt{5}$ | D. | 3÷$\sqrt{\frac{2}{3}}$=$\frac{3}{2}\sqrt{6}$ |
3.已知抛物线y=-x2-2x+3与x轴交于A、B两点,将这条抛物线的顶点记为C,连接AC、BC,则tan∠CAB的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | 2 |
7.若点O是等腰△ABC的外心,且∠BOC=60°,底边BC=2,则△ABC的面积为( )
| A. | 2+$\sqrt{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | 2+$\sqrt{3}$或2-$\sqrt{3}$ | D. | 4+2$\sqrt{3}$或2-$\sqrt{3}$ |
4.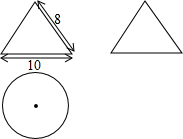 如图,按照三视图确定该几何体的全面积是(图中尺寸单位:cm)( )
如图,按照三视图确定该几何体的全面积是(图中尺寸单位:cm)( )
 如图,按照三视图确定该几何体的全面积是(图中尺寸单位:cm)( )
如图,按照三视图确定该几何体的全面积是(图中尺寸单位:cm)( )| A. | 40πcm2 | B. | 65πcm2 | C. | 80πcm2 | D. | 105πcm2 |
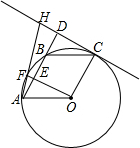 如图,A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作OF的平行线交AB的延长线于点D,延长AF交直线CD于点H.
如图,A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作OF的平行线交AB的延长线于点D,延长AF交直线CD于点H. 已知:如图,⊙O是△ABC的外接圆,$\widehat{AB}$=$\widehat{AC}$,点D在边BC上,AE∥BC,AE=BD.
已知:如图,⊙O是△ABC的外接圆,$\widehat{AB}$=$\widehat{AC}$,点D在边BC上,AE∥BC,AE=BD.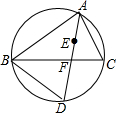 如图,点E是△ABC的内心,AE的延长线与BC相交于点F,与△ABC的外接圆相交于点D
如图,点E是△ABC的内心,AE的延长线与BC相交于点F,与△ABC的外接圆相交于点D