题目内容
7.若点O是等腰△ABC的外心,且∠BOC=60°,底边BC=2,则△ABC的面积为( )| A. | 2+$\sqrt{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | 2+$\sqrt{3}$或2-$\sqrt{3}$ | D. | 4+2$\sqrt{3}$或2-$\sqrt{3}$ |
分析 根据题意可以画出相应的图形,然后根据不同情况,求出相应的边的长度,从而可以求出不同情况下△ABC的面积,本题得以解决.
解答  解:由题意可得,如右图所示
解:由题意可得,如右图所示
存在两种情况,
当△ABC为△A1BC时,连接OB、OC,
∵点O是等腰△ABC的外心,且∠BOC=60°,底边BC=2,OB=OC,
∴△OBC为等边三角形,OB=OC=BC=2,OA1⊥BC于点D,
∴CD=1,OD=$\sqrt{{2}^{2}-{1}^{2}}=\sqrt{3}$,
∴${S}_{△{A}_{1}BC}=\frac{BC•{A}_{1}D}{2}=\frac{2×(2-\sqrt{3})}{2}$=2-$\sqrt{3}$,
当△ABC为△A2BC时,连接OB、OC,
∵点O是等腰△ABC的外心,且∠BOC=60°,底边BC=2,OB=OC,
∴△OBC为等边三角形,OB=OC=BC=2,OA1⊥BC于点D,
∴CD=1,OD=$\sqrt{{2}^{2}-{1}^{2}}=\sqrt{3}$,
∴S△A2BC=$\frac{BC•D{A}_{2}}{2}$=$\frac{2×(2+\sqrt{3})}{2}$=2+$\sqrt{3}$,
由上可得,△ABC的面积为$2-\sqrt{3}$或2+$\sqrt{3}$,
故选C.
点评 本题考查三角形的外接圆和外心,等腰三角形的性质,解题的关键是明确题意,找出所求问题需要的条件,利用分类讨论的数学思想解答问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.为了提高学生书写汉字的能力,增强保护汉字的意识,某校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为x(分),且50≤x<100,将其按分数段分为五组,绘制出以下不完整表格:
请根据表格提供的信息,解答以下问题:
(1)本次决赛共有50名学生参加;
(2)直接写出表中a=16,b=0.28;
(3)请补全下面相应的频数分布直方图;
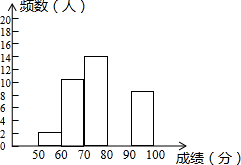
(4)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为48%.
| 组别 | 成绩x(分) | 频数(人数) | 频率 |
| 一 | 50≤x<60 | 2 | 0.04 |
| 二 | 60≤x<70 | 10 | 0.2 |
| 三 | 70≤x<80 | 14 | b |
| 四 | 80≤x<90 | a | 0.32 |
| 五 | 90≤x<100 | 8 | 0.16 |
(1)本次决赛共有50名学生参加;
(2)直接写出表中a=16,b=0.28;
(3)请补全下面相应的频数分布直方图;

(4)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为48%.
12. 如图,在Rt△ABC中,∠C=90°,AC=4,BC=7,点D在边BC上,CD=3,⊙A的半径长为3,⊙D与⊙A相交,且点B在⊙D外,那么⊙D的半径长r的取值范围是( )
如图,在Rt△ABC中,∠C=90°,AC=4,BC=7,点D在边BC上,CD=3,⊙A的半径长为3,⊙D与⊙A相交,且点B在⊙D外,那么⊙D的半径长r的取值范围是( )
 如图,在Rt△ABC中,∠C=90°,AC=4,BC=7,点D在边BC上,CD=3,⊙A的半径长为3,⊙D与⊙A相交,且点B在⊙D外,那么⊙D的半径长r的取值范围是( )
如图,在Rt△ABC中,∠C=90°,AC=4,BC=7,点D在边BC上,CD=3,⊙A的半径长为3,⊙D与⊙A相交,且点B在⊙D外,那么⊙D的半径长r的取值范围是( )| A. | 1<r<4 | B. | 2<r<4 | C. | 1<r<8 | D. | 2<r<8 |
19.某校规定学生的学期数学成绩满分为100分,其中研究性学习成绩占40%,期末卷面成绩占60%,小明的两项成绩(百分制)依次是80分,90分,则小明这学期的数学成绩是( )
| A. | 80分 | B. | 82分 | C. | 84分 | D. | 86分 |
17.下列计算正确的是( )
| A. | x4+x4=2x8 | B. | x3•x2=x6 | C. | (x2y)3=x6y3 | D. | (x-y)(y-x)=x2-y2 |
 如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:
如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论: 有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,历时7分钟同时到达C点,乙机器人始终以60米/分的速度行走,如图是甲、乙两机器人之间的距离y(米)与他们的行走时间x(分钟)之间的函数图象,请结合图象,回答下列问题:
有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,历时7分钟同时到达C点,乙机器人始终以60米/分的速度行走,如图是甲、乙两机器人之间的距离y(米)与他们的行走时间x(分钟)之间的函数图象,请结合图象,回答下列问题: