13.为提高饮水质量,越来越多的居民选购家用净水器,一商场抓住商机,从厂家购进了A,B两种型号家用净水器,其数量和进价如表:
为使每台B型号家用净水器的售价是A型号的2倍,且保证售完这批家用净水器的利润不低于1650元,每台A型号家用净水器的售价至少应为多少元?(注:利润=售价-进价)
0 281958 281966 281972 281976 281982 281984 281988 281994 281996 282002 282008 282012 282014 282018 282024 282026 282032 282036 282038 282042 282044 282048 282050 282052 282053 282054 282056 282057 282058 282060 282062 282066 282068 282072 282074 282078 282084 282086 282092 282096 282098 282102 282108 282114 282116 282122 282126 282128 282134 282138 282144 282152 366461
| 型号 | 数量(台) | 进价(元/台) |
| A | 10 | 150元 |
| B | 5 | 350元 |
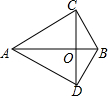 如图,△ABC中,∠ACB=90°,∠BAC=30°,将线段AC绕点A顺时针旋转60°得到线段AD,连接CD交AB于点O,连接BD.
如图,△ABC中,∠ACB=90°,∠BAC=30°,将线段AC绕点A顺时针旋转60°得到线段AD,连接CD交AB于点O,连接BD.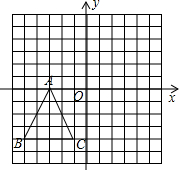 如图,在平面直角坐标系内,△ABC三个顶点的坐标分别为A(-3,0),B(-5,-4),C(-1,-4).
如图,在平面直角坐标系内,△ABC三个顶点的坐标分别为A(-3,0),B(-5,-4),C(-1,-4). 解不等式组:$\left\{\begin{array}{l}{3(x-2)≤x-4}\\{\frac{1+2x}{3}>x-1}\end{array}\right.$并将其解集表示在如图所示的数轴上.
解不等式组:$\left\{\begin{array}{l}{3(x-2)≤x-4}\\{\frac{1+2x}{3}>x-1}\end{array}\right.$并将其解集表示在如图所示的数轴上.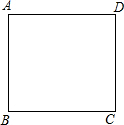 如图是一张边长为3cm的正方形纸片ABCD.现要利用这张正方形纸片剪出一个腰长为2cm的等腰三角形,要求等腰三角形的一个顶点与正方形的一个顶点重合,另外两个顶点都在正方形的边上,则剪下的等腰三角形的面积为2或$\sqrt{3}$cm2.
如图是一张边长为3cm的正方形纸片ABCD.现要利用这张正方形纸片剪出一个腰长为2cm的等腰三角形,要求等腰三角形的一个顶点与正方形的一个顶点重合,另外两个顶点都在正方形的边上,则剪下的等腰三角形的面积为2或$\sqrt{3}$cm2. 如图,已知一次函数y=kx+b的图象与x轴交于点(3,0),与y轴交于点(0,2),不等式kx+b≥2解集是x≤0.
如图,已知一次函数y=kx+b的图象与x轴交于点(3,0),与y轴交于点(0,2),不等式kx+b≥2解集是x≤0.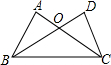 如图,△ABC和△DCB中,∠A=∠D=90°,边AC与DB相交于点O,要使△ABC≌△DCB,则需要添加的一个条件是AB=DC.(写出一种情况即可)
如图,△ABC和△DCB中,∠A=∠D=90°,边AC与DB相交于点O,要使△ABC≌△DCB,则需要添加的一个条件是AB=DC.(写出一种情况即可)
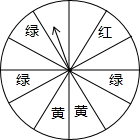 某餐厅为了吸引顾客,举行吃套餐优惠活动,套餐每套20元,每消费一套即可直接获得10元餐劵,或者参与游戏赢得餐劵.游戏规则如下:设立了一个可以自由转动的转盘(如图,转盘被平均分成12份),顾客每消费一套套餐,就可以获得一次转动转盘的机会,如果转盘停止后,指针正好对准红色、黄色、绿色、空白区域,那么顾客就可以分别获得20元、15元、10元、5元餐劵,下次就餐时可以代替现金消费.
某餐厅为了吸引顾客,举行吃套餐优惠活动,套餐每套20元,每消费一套即可直接获得10元餐劵,或者参与游戏赢得餐劵.游戏规则如下:设立了一个可以自由转动的转盘(如图,转盘被平均分成12份),顾客每消费一套套餐,就可以获得一次转动转盘的机会,如果转盘停止后,指针正好对准红色、黄色、绿色、空白区域,那么顾客就可以分别获得20元、15元、10元、5元餐劵,下次就餐时可以代替现金消费.