题目内容
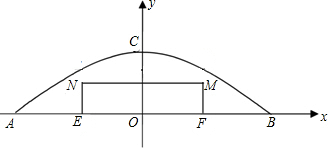
6.某公园有一个抛物线形状的观景拱桥ACB,其横截面如图所示,量得该拱桥占地面最宽处AB=20米,最高处点C距地面5米(即OC=5米)(1)分别以AB、OC所在直线为x轴、y轴,建立如图所示的平面直角坐标系,求该抛物线的解析式;
(2)夜晚,公园沿着抛物线ACB用彩灯勾勒拱桥的形状;现公园管理处打算在观景拱桥ABC的横截面前放置一个长为10米的矩形广告牌EFMN,为安全起见,要求广告牌离拱桥的桥面至少0.35米,求矩形广告牌的最大高度,并说明理由.
分析 (1)根据题意可设抛物线解析式为y=ax2+c,将点C(0,5),点B(10,0)代入求得a、c的值即可求解;
(2)令x=5求得y的值,将y的值减去0.35可得广告牌最大高度.
解答 解:(1)根据题意,设抛物线解析式为y=ax2+c,
将点C(0,5),点B(10,0)代入,得:
$\left\{\begin{array}{l}{100a+c=0}\\{c=5}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{20}}\\{c=5}\end{array}\right.$.
故抛物线解析式为:y=-$\frac{1}{20}$x2+5;
(2)当x=5时,y=-$\frac{1}{20}$×25+5=3.75(m),
3.75-0.35=3.4(m).
答:矩形广告牌的最大高度为3.4m.
点评 本题主要考查二次函数的实际应用,根据题意设出函数解析式是根本,待定系数法求得抛物线解析式是解题关键.

练习册系列答案
相关题目
17.下列说法正确的是( )
| A. | $\sqrt{4}$是无理数 | B. | $\sqrt{16}$的平方根是±4 | C. | 0的相反数是0 | D. | -0.5的倒数是2 |
1.如图是某班全体学生外出时乘车、步行、骑车的人数分布直方图和扇形统计图,(两图都不完整),则下列结论中正确的是( )


| A. | 步行人数为30人 | B. | 骑车人数占总人数的10% | ||
| C. | 该班总人数为50人 | D. | 乘车人数是骑车人数的40% |
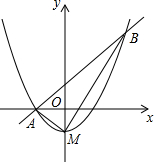 如图,顶点M(0,-1)在y轴上的抛物线与直线y=x+1相交于A,B两点,且点A在x轴上,连结AM,BM.
如图,顶点M(0,-1)在y轴上的抛物线与直线y=x+1相交于A,B两点,且点A在x轴上,连结AM,BM. 解不等式组:$\left\{\begin{array}{l}{3(x-2)≤x-4}\\{\frac{1+2x}{3}>x-1}\end{array}\right.$并将其解集表示在如图所示的数轴上.
解不等式组:$\left\{\begin{array}{l}{3(x-2)≤x-4}\\{\frac{1+2x}{3}>x-1}\end{array}\right.$并将其解集表示在如图所示的数轴上.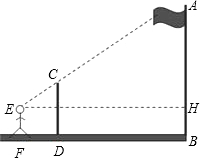 九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,如图所示,已知标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,则旗杆AB的高度13.5m.
九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,如图所示,已知标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,则旗杆AB的高度13.5m.