题目内容
10.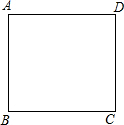 如图是一张边长为3cm的正方形纸片ABCD.现要利用这张正方形纸片剪出一个腰长为2cm的等腰三角形,要求等腰三角形的一个顶点与正方形的一个顶点重合,另外两个顶点都在正方形的边上,则剪下的等腰三角形的面积为2或$\sqrt{3}$cm2.
如图是一张边长为3cm的正方形纸片ABCD.现要利用这张正方形纸片剪出一个腰长为2cm的等腰三角形,要求等腰三角形的一个顶点与正方形的一个顶点重合,另外两个顶点都在正方形的边上,则剪下的等腰三角形的面积为2或$\sqrt{3}$cm2.
分析 分类讨论:顶角的顶点是正方形的顶点,顶角的顶点在正方形的边上,根据勾股定理,可得答案.
解答 解:①如图,角的顶点是正方形的顶点,
AC=AB=2cm,
则剪下的等腰三角形的面积为:$\frac{1}{2}$×2×2=2(cm2);
②顶角的顶点在正方形的边上,
∵AB=BC=2,
∴BD=1.
在直角△BCD中,由勾股定理得到CD=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$(cm),
则剪下的等腰三角形的面积为:$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$(cm2).
综上所述,剪下的等腰三角形的面积为2cm2或$\sqrt{3}$cm2.
故答案是:2或$\sqrt{3}$.
点评 本题考查了勾股定理,利用了勾股定理,分类讨论时解题关键,以防遗漏.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
19.下列运算正确的是( )
| A. | a2+a2=2a2 | B. | a6•a4=a24 | C. | a4+b4=(a+b)4 | D. | (x3)3=x6 |
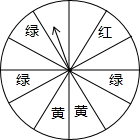 某餐厅为了吸引顾客,举行吃套餐优惠活动,套餐每套20元,每消费一套即可直接获得10元餐劵,或者参与游戏赢得餐劵.游戏规则如下:设立了一个可以自由转动的转盘(如图,转盘被平均分成12份),顾客每消费一套套餐,就可以获得一次转动转盘的机会,如果转盘停止后,指针正好对准红色、黄色、绿色、空白区域,那么顾客就可以分别获得20元、15元、10元、5元餐劵,下次就餐时可以代替现金消费.
某餐厅为了吸引顾客,举行吃套餐优惠活动,套餐每套20元,每消费一套即可直接获得10元餐劵,或者参与游戏赢得餐劵.游戏规则如下:设立了一个可以自由转动的转盘(如图,转盘被平均分成12份),顾客每消费一套套餐,就可以获得一次转动转盘的机会,如果转盘停止后,指针正好对准红色、黄色、绿色、空白区域,那么顾客就可以分别获得20元、15元、10元、5元餐劵,下次就餐时可以代替现金消费.