��Ŀ����
7�������һ��ƽ��ͼ�Σ������ֱ�ߺ�Բ�澭��������ͼ����Ƴ߹���ͼ��������һ����������ص������ȣ���ƵȻ�������ô�����ĵȻ�ת����Ϊ�صġ���������
��1���Ķ����
��ͼ�٣���֪����ABCD���ӳ�AD��E��ʹDE=DC����AEΪֱ������Բ���ӳ�CD����Բ�ڵ�H����DHΪ����������DFGH����������DFFH��ABCD�Ȼ���
���ɣ�����AH��EH��
��AEΪֱ�����AHE=90����HAE+��HEA=90�㣮
��DH��AE���ADH=��EDH=90��
���HAD+��AHD=90��
���AHD=��HED���ADH�ס�HDE��
��$\frac{AD}{DH}=\frac{DH}{DE}$����DH2=AD��DE��
�֡�DE=DC��DH2=AD��DC����������DFGH�����ABCD�Ȼ���
��2�����˼��
ƽ���ı��εġ�������˼·�ǣ��Ȱ�ƽ���ı���ת��Ϊ�Ȼ��ľ��Σ��ٰѾ���ת��Ϊ�Ȼ��������Σ�
��3���������
�����εġ�������˼·�ǣ��Ȱ�������ת��Ϊ�Ȼ��ľ��Σ���дͼ�θ��ƣ�����ת��Ϊ�Ȼ��������Σ�
��ͼ�ڣ���ABC�Ķ���������������ĸ���ϣ����ó߹������������ABC�Ȼ��������ε�һ���ߣ�
����Ҫ��д������������Ҫ������ͼ�ۼ���
��4����չ̽��
n���Σ�n��3���ġ�������˼·֮һ�ǣ���n����ת��Ϊn-1���Σ�����ֱ��ת��Ϊ�Ȼ������Σ��Ӷ����Ի�����
��ͼ�ۣ��ı���ABCD�Ķ���������������ĸ���ϣ����ó߹����������������ı���ABCD�Ȼ��������Σ���Ҫ��д������������Ҫ������ͼ�ۼ�����
���� ��1�����ȸ������������ε��ж��������ɵá�ADH�ס�HDE��Ȼ����ݵ����������ɵ�DH2=AD��DC���ݴ��жϼ��ɣ�
��3�������������εĵ�Ϊ���εij����������εĸߵ�һ��Ϊ���εĿ�������ABCת��Ϊ�Ȼ��ľ���MBCD��Ȼ���ӳ�MD��E��ʹDE=DC����MEΪֱ������Բ���ӳ�CD����Բ�ڵ�H����DH��Ϊ���ABC�Ȼ��������ε�һ���ߣ�
��4�����ȸ���AG��EH���жϳ�AG=2EH��Ȼ�����CF=2DF���ɵ�CF•EH=DF•AG���ݴ��жϳ�S��CEF=S��ADF��S��CDI=S��AEI������S��BCE=S�ı���ABCD������BCE���ı���ABCD�Ȼ����ݴ˽�ɣ�
��� 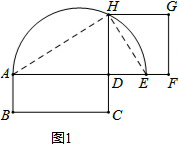 �⣺��1����ͼ�٣�����AH��EH��
�⣺��1����ͼ�٣�����AH��EH��
��AEΪֱ����
���AHE=90�㣬
���HAE+��HEA=90�㣮
��DH��AE��
���ADH=��EDH=90�㣬
���HAD+��AHD=90�㣬
���AHD=��HED��
���ADH�ס�HDE��
��$\frac{AD}{DH}$=$\frac{DH}{DE}$��
��DH2=AD��DE��
�֡�DE=DC��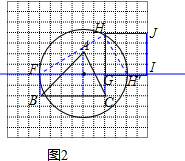
��DH2=AD��DC��
��������DFGH�����ABCD�Ȼ���
��3����ͼ2��������
�ٹ�A����AD��ֱBC��D��
����AD�Ĵ�ֱƽ���ߣ�ȡAD�е�E��
�۹�E��BCƽ���ߣ���������BCGF����S����BCGF=S��ABC��
��������ͬ��2����������Ȼ������Σ�
��4����ͼ3��������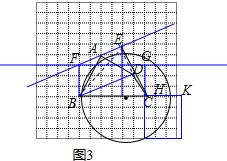
�ٹ�A����BDƽ����l��
���ӳ�CD��ƽ������E�㣻
������BE����S�ı���ABCD=S��EBC��
ͬ��3����������Ȼ������Σ�
��BCE���ı���ABCD�Ȼ����������£�
��BD��l��
��S��ABD=S��EBD��
��S��BCE=S�ı���ABCD��
����EBC���ı���ABCD�Ȼ���
�ʴ�Ϊ����HDE��AD��DC�����Σ�
���� ��1��������Ҫ�������������ۺ��⣬�����˷������������������˷�������˼���Ӧ�ã����������ν��˼���Ӧ�ã�Ҫ�������գ�
��2����������˾��Ρ������ε���������Լ��ԵȻ�ת�������⣬Ҫ�������գ�

 ��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д�
��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д� ȫ�̽��ϵ�д�
ȫ�̽��ϵ�д�| A�� | 3a+2b=5ab | B�� | ��a+2b��2=a2+4b2 | C�� | a2•a3=a5 | D�� | 4x2y-2xy2=2xy |
| A�� | x1=x2=5 | B�� | x1=x2=0 | C�� | x1=0��x2=5 | D�� | x1=-5��x2=0 |
 ƽ���ϣ����߳���ȵ��������Ρ������Ρ��������ε�һ���غϲ�����һ����ͼ�����1+��2+��3=60�㣮
ƽ���ϣ����߳���ȵ��������Ρ������Ρ��������ε�һ���غϲ�����һ����ͼ�����1+��2+��3=60�㣮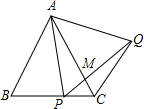 ��ͼ���ڡ�ABCΪ�ȱ������Σ�PΪBC��һ�㣬��APQΪ�ȱ������Σ�PQ��AC�ཻ�ڵ�M�������н�������ȷ���ǣ�������
��ͼ���ڡ�ABCΪ�ȱ������Σ�PΪBC��һ�㣬��APQΪ�ȱ������Σ�PQ��AC�ཻ�ڵ�M�������н�������ȷ���ǣ�������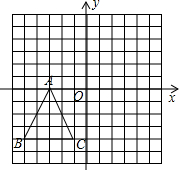 ��ͼ����ƽ��ֱ������ϵ�ڣ���ABC�������������ֱ�ΪA��-3��0����B��-5��-4����C��-1��-4����
��ͼ����ƽ��ֱ������ϵ�ڣ���ABC�������������ֱ�ΪA��-3��0����B��-5��-4����C��-1��-4���� ��֪����ABC
��֪����ABC