题目内容
14.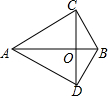 如图,△ABC中,∠ACB=90°,∠BAC=30°,将线段AC绕点A顺时针旋转60°得到线段AD,连接CD交AB于点O,连接BD.
如图,△ABC中,∠ACB=90°,∠BAC=30°,将线段AC绕点A顺时针旋转60°得到线段AD,连接CD交AB于点O,连接BD.(1)求证:AB垂直平分CD;
(2)若AB=6,求BD的长.
分析 (1)根据旋转的性质得到△ACD是等边三角形,根据线段垂直平分线的概念判断即可;
(2)根据直角三角形的性质计算即可.
解答 (1)证明:∵线段AC绕点A顺时针旋转60°得到线段AD,
∴AD=AC,∠CAD=60°,
∴△ACD是等边三角形,
∵∠BAC=30°,
∴∠DAB=30°,
∴∠BAC=∠DAB,
∴AO⊥CD,又CO=DO,
∴AB垂直平分CD;
(2)解:∵AB垂直平分CD,
∴BD=BC,∠ADB=∠ACB=90°,
∴BD=$\frac{1}{2}$AB=3.
点评 本题考查的是线段垂直平分线的判定、直角三角形的性质,掌握直角三角形中,30°角所对的直角边等于斜边的一半是解题的关键.

练习册系列答案
相关题目
2.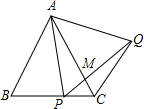 如图,在△ABC为等边三角形,P为BC上一点,△APQ为等边三角形,PQ与AC相交于点M,则下列结论中正确的是( )
如图,在△ABC为等边三角形,P为BC上一点,△APQ为等边三角形,PQ与AC相交于点M,则下列结论中正确的是( )
①AB∥CQ;②∠ACQ=60°;③AP2=AM•AC;④若BP=PC,则PQ⊥AC.
 如图,在△ABC为等边三角形,P为BC上一点,△APQ为等边三角形,PQ与AC相交于点M,则下列结论中正确的是( )
如图,在△ABC为等边三角形,P为BC上一点,△APQ为等边三角形,PQ与AC相交于点M,则下列结论中正确的是( )①AB∥CQ;②∠ACQ=60°;③AP2=AM•AC;④若BP=PC,则PQ⊥AC.
| A. | 只有①② | B. | 只有①③ | C. | 只有①②③ | D. | ①②③④ |
6.在平面直角坐标系中,点P(-3,2)关于直线y=x对称点的坐标是( )
| A. | (-3,-2) | B. | (3,2) | C. | (2,-3) | D. | (3,-2) |
3.已知:2m+3n=5,则4m•8n=( )
| A. | 16 | B. | 25 | C. | 32 | D. | 64 |
4.计算:(-2a)2•(-3a)3的结果是( )
| A. | -108a5 | B. | -108a6 | C. | 108a5 | D. | 108a6 |
 如图,边长等于4的正方形ABCD两个顶点A与D分别在x轴和y轴上滑动(A、D都不与坐标原点O重合),作CE⊥x轴,垂足为E,当OA等于2$\sqrt{2}$时,四边形OACE面积最大.
如图,边长等于4的正方形ABCD两个顶点A与D分别在x轴和y轴上滑动(A、D都不与坐标原点O重合),作CE⊥x轴,垂足为E,当OA等于2$\sqrt{2}$时,四边形OACE面积最大. 如图,已知一次函数y=kx+b的图象与x轴交于点(3,0),与y轴交于点(0,2),不等式kx+b≥2解集是x≤0.
如图,已知一次函数y=kx+b的图象与x轴交于点(3,0),与y轴交于点(0,2),不等式kx+b≥2解集是x≤0.