题目内容
11. 解不等式组:$\left\{\begin{array}{l}{3(x-2)≤x-4}\\{\frac{1+2x}{3}>x-1}\end{array}\right.$并将其解集表示在如图所示的数轴上.
解不等式组:$\left\{\begin{array}{l}{3(x-2)≤x-4}\\{\frac{1+2x}{3}>x-1}\end{array}\right.$并将其解集表示在如图所示的数轴上.
分析 分别求出每一个不等式的解集,根据解集在数轴上的表示确定不等式组的解集.
解答 解:解不等式3(x-2)≤x-4,得:x≤1,
解不等式$\frac{1+2x}{3}>x-1$,得:x<4,
所以不等式组的解集为:x≤1,
其解集在数轴上表示为: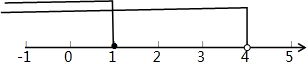
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
1.下列命题中,
①三角形的外心是三角形三边垂直平分线的交点;
②函数y=(1-a)x2-4x+6与x轴只有一个交点,则a=$\frac{1}{3}$;
③半径分别为1和2的两圆相切,则圆心距为3;
④若对于任意x>1的实数,都有ax>1成立,则a≥1.
其中正确的个数有( )
①三角形的外心是三角形三边垂直平分线的交点;
②函数y=(1-a)x2-4x+6与x轴只有一个交点,则a=$\frac{1}{3}$;
③半径分别为1和2的两圆相切,则圆心距为3;
④若对于任意x>1的实数,都有ax>1成立,则a≥1.
其中正确的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.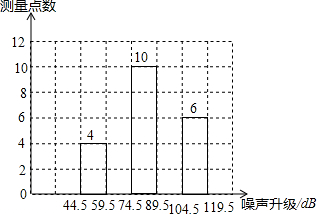 为了增强人们的环境保护意识,某校若干名学生组成了“控制噪声污染”课题学习研究小组.在环保局工作人员帮助指导下,该小组抽样调查了全市40个噪声测量点在某时刻的噪声声级(单位:dB),并将调查的数据进行处理(设所测数据是正整数),得频数分布表如下:
为了增强人们的环境保护意识,某校若干名学生组成了“控制噪声污染”课题学习研究小组.在环保局工作人员帮助指导下,该小组抽样调查了全市40个噪声测量点在某时刻的噪声声级(单位:dB),并将调查的数据进行处理(设所测数据是正整数),得频数分布表如下:
根据表中提供的信息解答下列问题:
(1)表中的c值为0.3;
(2)补全频数分布直方图;
(3)如果全市共有200个测量点,那么在这一时刻噪声声级小于75dB的测量点约有多少个?
 为了增强人们的环境保护意识,某校若干名学生组成了“控制噪声污染”课题学习研究小组.在环保局工作人员帮助指导下,该小组抽样调查了全市40个噪声测量点在某时刻的噪声声级(单位:dB),并将调查的数据进行处理(设所测数据是正整数),得频数分布表如下:
为了增强人们的环境保护意识,某校若干名学生组成了“控制噪声污染”课题学习研究小组.在环保局工作人员帮助指导下,该小组抽样调查了全市40个噪声测量点在某时刻的噪声声级(单位:dB),并将调查的数据进行处理(设所测数据是正整数),得频数分布表如下:| 组 别 | 噪声声级分组 | 频 数 | 频 率 |
| 1 | 44.5--59.5 | 4 | 0.1 |
| 2 | 59.5--74.5 | a | 0.2 |
| 3 | 74.5--89.5 | 10 | 0.25 |
| 4 | 89.5--104.5 | b | c |
| 5 | 104.5-119.5 | 6 | 0.15 |
| 合 计 | 40 | 1.00 |
(1)表中的c值为0.3;
(2)补全频数分布直方图;
(3)如果全市共有200个测量点,那么在这一时刻噪声声级小于75dB的测量点约有多少个?
 请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.
请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.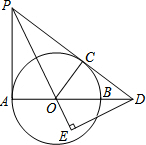 已知,如图,AB为⊙O的直径,PD切⊙O于点C,与AB的延长线交于点D,DE⊥PO交PO延长线于点E,连接PA,且∠EDB=∠EPA.
已知,如图,AB为⊙O的直径,PD切⊙O于点C,与AB的延长线交于点D,DE⊥PO交PO延长线于点E,连接PA,且∠EDB=∠EPA.
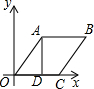
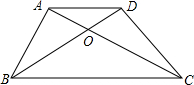 如图,梯形ABCD中,OD:OB=2:3,三角形AOB的面积是6平方厘米,求梯形ABCD的面积.
如图,梯形ABCD中,OD:OB=2:3,三角形AOB的面积是6平方厘米,求梯形ABCD的面积.