题目内容
7.先化简再求值:$\frac{x-y}{x}$÷(x-$\frac{2xy-{y}^{2}}{x}$),其中x=2015,y=2014.分析 先将括号内进行通分,然后将除法运算转化为乘法运算,最后将x=2015,y=2014代入化简后的式子,就可解决问题.
解答 解:∵x=2015,y=2014,
∴原式=$\frac{x-y}{x}$÷$\frac{{x}^{2}-2xy+{y}^{2}}{x}$
=$\frac{x-y}{x}$•$\frac{x}{(x-y)^{2}}$
=$\frac{1}{x-y}$
=$\frac{1}{2015-2014}$
=1.
点评 本题主要考查的是分式的混合运算、因式分解等知识,进行分式的乘法运算时,通常先将分子和分母因式分解,然后再约分,从而达到化简的目的.

练习册系列答案
相关题目
19.下列方程与方程2x2-x-2=0同解的是( )
| A. | (x-$\frac{1}{2}$)2=$\frac{5}{4}$ | B. | (x-$\frac{1}{2}$)2=$\frac{1}{4}$ | C. | (x-$\frac{1}{4}$)2=$\frac{9}{16}$ | D. | (x-$\frac{1}{4}$)2=$\frac{17}{16}$ |
 已知如图,∠ABC=∠ACB,BD⊥AC,CE⊥AB,垂足分别是D,E,求证:△BCD≌△CBE.
已知如图,∠ABC=∠ACB,BD⊥AC,CE⊥AB,垂足分别是D,E,求证:△BCD≌△CBE.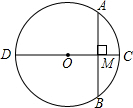 已知:如图,CD为⊙O的直径,AB为⊙O的弦.CD⊥AB,垂足为M,求证:AC=BC.
已知:如图,CD为⊙O的直径,AB为⊙O的弦.CD⊥AB,垂足为M,求证:AC=BC.