题目内容
18．
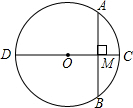已知：如图，CD为⊙O的直径，AB为⊙O的弦．CD⊥AB，垂足为M，求证：AC=BC．
分析 由于CD为⊙O的直径，CD⊥AB，根据垂径定理得到$\widehat{AC}$=$\widehat{BC}$，再根据圆心角、弧、弦的关系由$\widehat{AC}$=$\widehat{BC}$得AC=BC．
解答 
解：∵CD为⊙O的直径，CD⊥AB，
∴$\widehat{AC}$=$\widehat{BC}$，
∴AC=BC．
点评 本题考查了垂径定理：平分弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了圆周角定理．
练习册系列答案
相关题目
9．已知点G是等边△ABC的重心，AB=6，P为AB边上的一个动点，则P、G两点间距离的最小值是（ ）
| A． | 2 | B． | $\frac{{\sqrt{3}}}{2}$ | C． | $\sqrt{3}$ | D． | $2\sqrt{3}$ |
如图，点D在∠BAC的角平分线上，DM⊥AB，垂足为M，DN⊥AC交AC的延长线于N，且BM=CN．求证：△ADM≌△ADN．
如图，△ABC内接⊙O中，AB=AC=5cm，BC=6cm，求⊙O的半径．
如图，一河坝的横断面为梯形，BC∥AD，AB=CD，坝顶宽BC是10米，坝高12米，斜坡AB的坡度为$\frac{2}{3}$，求坝底AD的长度．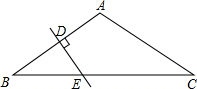
如图，在△ABC中，∠A=120°，AB=AC，AB的垂直平分线DE与AB，BC分别交于点D和E．若BE=3，试求CE的长．
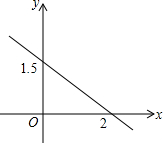根据所给的函数图象．求出相应的函数关系式．
如图，已知△ABC中，AB＞AC，BD是AC边上中线，CE是AB边上中线，且BD⊥CE于点G，GF⊥BC于点F，若GF=2$\sqrt{2}$，BC=6，求AB的长．