题目内容
10.已知∠EOF=90°,过O点作射线OM,且∠MOF为锐角,OA平分∠MOE,OB平分∠FOM.求∠AOB的大小.分析 首先根据题意画出图形,然后根据角平分线的定义以及角的和差关系求解即可.
解答 解:如图1所示:
根据图形可知:∠EOM=∠EOF+∠FOM=90°+∠FOM,
∵OA平分∠EOM,
∴∠AOM=$\frac{1}{2}∠EOM$=$\frac{1}{2}(90°+∠FOM)$=45°+$\frac{1}{2}∠FOM$.
∵OB平分∠FOM,
∴∠BOM=$\frac{1}{2}∠FOM$.
∴∠AOB=∠AOM-∠BOM=45$°+\frac{1}{2}∠FOM-\frac{1}{2}∠FOM$=45°.
如图2所示:
∵OA平分∠EOM,
∴∠AOM=$\frac{1}{2}$∠EOM.
∵OB平分∠MOF,
∴∠MOB=$\frac{1}{2}∠MOF$.
∴∠AOB=$\frac{1}{2}$∠EOM+$\frac{1}{2}$∠MOF=$\frac{1}{2}∠EOF$=$\frac{1}{2}×90°$=45°.
综上所述,∠AOB=45°.
点评 本题主要考查的是角平分线的定义、角的比较与运算,根据题意画出图形是解题的关键.

练习册系列答案
相关题目
20.求半径为2的圆的内接正三角形,正方形,正六边形的边长、边心距、中心角和面积.将结果填写在下表中:
| 圆的内接正多边形 | 边长 | 边心距 | 中心角 | 面积 |
| 正三角形 | $\sqrt{3}$ | 1 | 120° | 3$\sqrt{3}$ |
| 正方形 | 2$\sqrt{2}$ | $\sqrt{2}$ | 90° | 8 |
| 正六边形 | 2 | $\sqrt{3}$ | 60° | 6$\sqrt{3}$ |
19.下列方程与方程2x2-x-2=0同解的是( )
| A. | (x-$\frac{1}{2}$)2=$\frac{5}{4}$ | B. | (x-$\frac{1}{2}$)2=$\frac{1}{4}$ | C. | (x-$\frac{1}{4}$)2=$\frac{9}{16}$ | D. | (x-$\frac{1}{4}$)2=$\frac{17}{16}$ |
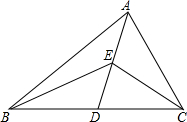 如图,在△ABC中,AD是中线,E是AD的中点,若△ABC的面积是24cm2,则△EBC的面积是12cm2.
如图,在△ABC中,AD是中线,E是AD的中点,若△ABC的面积是24cm2,则△EBC的面积是12cm2.