题目内容
1.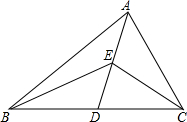 如图,在△ABC中,AD是中线,E是AD的中点,若△ABC的面积是24cm2,则△EBC的面积是12cm2.
如图,在△ABC中,AD是中线,E是AD的中点,若△ABC的面积是24cm2,则△EBC的面积是12cm2.
分析 根据AD是中线,于是得到S△ABD=S△ACD=$\frac{1}{2}$S△ABC=$\frac{1}{2}×24$=12cm2,由于E是AD的中点,于是得到S△CDE=$\frac{1}{2}$S△ACD=6cm2,S△BDE=$\frac{1}{2}$S△ABD=6cm2,即可得到结论.
解答 解:∵AD是中线,
∴S△ABD=S△ACD=$\frac{1}{2}$S△ABC=$\frac{1}{2}×24$=12cm2,
∵E是AD的中点,
∴S△CDE=$\frac{1}{2}$S△ACD=6cm2,
S△BDE=$\frac{1}{2}$S△ABD=6cm2,
∴△EBC的面积=S△CDE+S△BDE=12cm2.
故答案为:12cm2.
点评 本题主要考查了三角形面积的等积变换:若两个三角形的高(或底)相等,其中一个三角形的底(或高)是另一三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍.结合图形直观解答.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
9.已知点G是等边△ABC的重心,AB=6,P为AB边上的一个动点,则P、G两点间距离的最小值是( )
| A. | 2 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
 如图,长方形ABCD的对角线AC与BD相交于点O,以O为原点建立直角坐标系,使x轴和y轴分别与长方形两邻边平行.已知AD=9,AB=4,求:
如图,长方形ABCD的对角线AC与BD相交于点O,以O为原点建立直角坐标系,使x轴和y轴分别与长方形两邻边平行.已知AD=9,AB=4,求: 如图,点D在∠BAC的角平分线上,DM⊥AB,垂足为M,DN⊥AC交AC的延长线于N,且BM=CN.求证:△ADM≌△ADN.
如图,点D在∠BAC的角平分线上,DM⊥AB,垂足为M,DN⊥AC交AC的延长线于N,且BM=CN.求证:△ADM≌△ADN. 如图,△ABC内接⊙O中,AB=AC=5cm,BC=6cm,求⊙O的半径.
如图,△ABC内接⊙O中,AB=AC=5cm,BC=6cm,求⊙O的半径.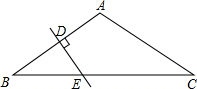 如图,在△ABC中,∠A=120°,AB=AC,AB的垂直平分线DE与AB,BC分别交于点D和E.若BE=3,试求CE的长.
如图,在△ABC中,∠A=120°,AB=AC,AB的垂直平分线DE与AB,BC分别交于点D和E.若BE=3,试求CE的长.