题目内容
20.求半径为2的圆的内接正三角形,正方形,正六边形的边长、边心距、中心角和面积.将结果填写在下表中:| 圆的内接正多边形 | 边长 | 边心距 | 中心角 | 面积 |
| 正三角形 | $\sqrt{3}$ | 1 | 120° | 3$\sqrt{3}$ |
| 正方形 | 2$\sqrt{2}$ | $\sqrt{2}$ | 90° | 8 |
| 正六边形 | 2 | $\sqrt{3}$ | 60° | 6$\sqrt{3}$ |
分析 在正△ABC中,连接OB、OC、作OM⊥BC于M,则∠BOC=120°,BM=CM,由等腰三角形的性质得出∠BOM=60°,∠OBM=30°,求出OM=$\frac{1}{2}$OB=1,BM=$\sqrt{3}$,即可求出面积;
在正方形ABCD中,连接OB、OC、作OM⊥BC于M,则∠BOC=90°,BM=CM,△OBC是等腰直角三角形,得出BC=2$\sqrt{2}$,OM=$\frac{1}{2}$BC=$\sqrt{2}$,求出正方形ABCD的面积=BC2即可;
在正六边形中,连接OA、OB,作OM⊥AB于M,则∠OAB=60°,证出△AOB是等边三角形,得出AB=OA=2,AM=BM=1,OM=$\sqrt{3}$AM=$\sqrt{3}$,求出正六边形的面积即可.
解答 解:在半径为2的圆的内接正三角形ABC中,如图1所示: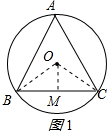
连接OB、OC、作OM⊥BC于M,
则∠BOC=$\frac{360°}{3}$=120°,BM=CM,
∵OB=OC,
∴∠BOM=60°,
∴∠OBM=30°,
∴OM=$\frac{1}{2}$OB=1,BM=$\sqrt{3}$OM=$\sqrt{3}$,
∴BC=2BM=2$\sqrt{3}$,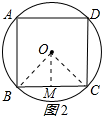
∴△ABC的面积=3×$\frac{1}{2}$×2$\sqrt{3}$×1=3$\sqrt{3}$;
在半径为2的圆的内接正方形ABCD中,如图2所示:
连接OB、OC、作OM⊥BC于M,
则∠BOC=$\frac{360°}{4}$=90°,BM=CM,△OBC是等腰直角三角形,
∴BC=$\sqrt{2}$OB=2$\sqrt{2}$,
∴OM=$\frac{1}{2}$BC=$\sqrt{2}$,
∴正方形ABCD的面积=BC2=(2$\sqrt{2}$)2=8;
在半径为2的圆的内接正六边形中,如图3所示: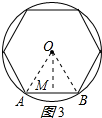
连接OA、OB,作OM⊥AB于M,
则∠OAB=$\frac{360°}{6}$=60°,
∵OA=OB,
∴△AOB是等边三角形,
∴AB=OA=2,AM=BM=1,
∴OM=$\sqrt{3}$AM=$\sqrt{3}$,
∴正六边形的面积=6×$\frac{1}{2}$×2×$\sqrt{3}$=6$\sqrt{3}$;
结果如下表:
| 圆的内接正多边形 | 边长 | 边心距 | 中心角 | 面积 |
| 正三角形 | $\sqrt{3}$ | 1 | 120° | 3$\sqrt{3}$ |
| 正方形 | 2$\sqrt{2}$ | $\sqrt{2}$ | 90° | 8 |
| 正六边形 | 2 | $\sqrt{3}$ | 60° | 6$\sqrt{3}$ |
点评 本题考查了正三角形的判定与性质、正方形的性质、正六边形的性质、等腰直角三角形的判定与性质;熟练掌握正多边形的性质是解决问题的关键.

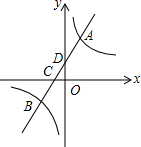 一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A(1,3),B(n,-2)两点,直线AB分别交x轴、y轴于D、C两点.
一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A(1,3),B(n,-2)两点,直线AB分别交x轴、y轴于D、C两点. 如图,按要求解答下列问题.
如图,按要求解答下列问题. 如图,在菱形ABCD中,AE和CF交于点G,且AE=CF.
如图,在菱形ABCD中,AE和CF交于点G,且AE=CF.