题目内容
15. 如图,⊙O内,弧AB等于弧CD,BP=5,求PD?
如图,⊙O内,弧AB等于弧CD,BP=5,求PD?
分析 根据已知条件$\widehat{AB}$=$\widehat{CD}$推知$\widehat{AD}$=$\widehat{BC}$,则AD=BC,通过全等三角形:△ADP≌△CBP,则其对应边相等:BP=PD.
解答  解:如图,连接AD,BC.
解:如图,连接AD,BC.
∵$\widehat{AB}$=$\widehat{CD}$,
∴$\widehat{AD}$=$\widehat{BC}$,
∴AD=BC.
在△ADP与△CBP中,
$\left\{\begin{array}{l}{∠APD=∠CPB}\\{∠ADP=∠CBP}\\{AD=CB}\end{array}\right.$,
∴△ADP≌△CBP(AAS),
∴BP=PD=5.
点评 本题考查了圆心角、弧、弦的关系.在证明∠ACP=∠DBP时,利用了圆周角定理:同弧所对的圆周角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,点D在∠BAC的角平分线上,DM⊥AB,垂足为M,DN⊥AC交AC的延长线于N,且BM=CN.求证:△ADM≌△ADN.
如图,点D在∠BAC的角平分线上,DM⊥AB,垂足为M,DN⊥AC交AC的延长线于N,且BM=CN.求证:△ADM≌△ADN. 如图,一河坝的横断面为梯形,BC∥AD,AB=CD,坝顶宽BC是10米,坝高12米,斜坡AB的坡度为$\frac{2}{3}$,求坝底AD的长度.
如图,一河坝的横断面为梯形,BC∥AD,AB=CD,坝顶宽BC是10米,坝高12米,斜坡AB的坡度为$\frac{2}{3}$,求坝底AD的长度.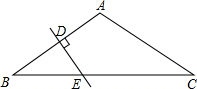 如图,在△ABC中,∠A=120°,AB=AC,AB的垂直平分线DE与AB,BC分别交于点D和E.若BE=3,试求CE的长.
如图,在△ABC中,∠A=120°,AB=AC,AB的垂直平分线DE与AB,BC分别交于点D和E.若BE=3,试求CE的长. 如图,在△ABC中,AD⊥BC于D,∠BAD=30°,∠C=45°,BD=1.
如图,在△ABC中,AD⊥BC于D,∠BAD=30°,∠C=45°,BD=1.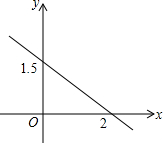 根据所给的函数图象.求出相应的函数关系式.
根据所给的函数图象.求出相应的函数关系式. 如图,点A、E、F、C在一条直线上,AE=CF,AD=BC,AD∥BC,求证:BE=DF.
如图,点A、E、F、C在一条直线上,AE=CF,AD=BC,AD∥BC,求证:BE=DF.