题目内容
20. 如图,在△ABC中,AD⊥BC于D,∠BAD=30°,∠C=45°,BD=1.
如图,在△ABC中,AD⊥BC于D,∠BAD=30°,∠C=45°,BD=1.(1)求AC的长.
(2)求△ABC的面积.
分析 (1)先根据直角三角形的性质求出AB的长,再由勾股定理求出AD的长,由等腰直角三角形的性质即可得出AD=CD,再由勾股定理可得出结论;
(2)根据三角形的面积公式可得出结论.
解答 解:(1)∵在△ABC中,AD⊥BC于D,∠BAD=30°,BD=1,
∴AB=2BD=2,
∴AD=$\sqrt{{AB}^{2}-{BD}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$.
∵∠C=45°,
∴△ADC是等腰直角三角形,
∴AD=CD=$\sqrt{3}$,
∴AC=$\sqrt{{AD}^{2}+{CD}^{2}}$=$\sqrt{{(\sqrt{3})}^{2}+{(\sqrt{3})}^{2}}$=$\sqrt{6}$;
(2)∵BD=1,由(1)知,AD=CD=$\sqrt{3}$,
∴S△ABC=$\frac{1}{2}$(BD+CD)•AD=$\frac{1}{2}$(1+$\sqrt{3}$)•$\sqrt{3}$=$\frac{\sqrt{3}+3}{2}$.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.若式子$\frac{3x-2}{2}$与$\frac{2x+1}{3}$的值相等,则x的值是( )
| A. | 1 | B. | $\frac{8}{5}$ | C. | $\frac{5}{8}$ | D. | 2 |
 如图,在△ABC中,D是BC上一点,∠1=∠2,∠BAC=68°,∠3=70°,求∠4的度数.
如图,在△ABC中,D是BC上一点,∠1=∠2,∠BAC=68°,∠3=70°,求∠4的度数. 如图,∠AOD=∠BOD=∠COE=90°.找出图中互补和互余的角,和∠BOE相等的角是哪个?
如图,∠AOD=∠BOD=∠COE=90°.找出图中互补和互余的角,和∠BOE相等的角是哪个? 如图,⊙O内,弧AB等于弧CD,BP=5,求PD?
如图,⊙O内,弧AB等于弧CD,BP=5,求PD?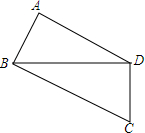 如图,在四边形ABCD中,BA⊥DA,AB=2,AD=2$\sqrt{3}$,CD=3,BC=5,求四边形ABCD的面积.
如图,在四边形ABCD中,BA⊥DA,AB=2,AD=2$\sqrt{3}$,CD=3,BC=5,求四边形ABCD的面积.