题目内容
3. 如图,一河坝的横断面为梯形,BC∥AD,AB=CD,坝顶宽BC是10米,坝高12米,斜坡AB的坡度为$\frac{2}{3}$,求坝底AD的长度.
如图,一河坝的横断面为梯形,BC∥AD,AB=CD,坝顶宽BC是10米,坝高12米,斜坡AB的坡度为$\frac{2}{3}$,求坝底AD的长度.
分析 先根据坡比求得AE的长,已知CB=10m,即可求得AD.
解答  解:过点C作CF⊥AD于点F,过点B作BE⊥AD于点E,
解:过点C作CF⊥AD于点F,过点B作BE⊥AD于点E,
∵四边形ABCD是等腰梯形,
∴AE=DF,
∵坝高BE=12米,斜坡AB的坡度为$\frac{2}{3}$,
∴$\frac{BE}{AE}$=$\frac{2}{3}$=$\frac{12}{AE}$,
解得:AE=18米,
∵BC=10米,
∴AD=2AE+BC=2×18+10=46(米),
答:坝底AD的长度为46米.
点评 此题考查了解直角三角形的应用中的坡度坡角的问题及等腰梯形的性质的掌握情况,将相关的知识点相结合更利于解题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 已知如图,∠ABC=∠ACB,BD⊥AC,CE⊥AB,垂足分别是D,E,求证:△BCD≌△CBE.
已知如图,∠ABC=∠ACB,BD⊥AC,CE⊥AB,垂足分别是D,E,求证:△BCD≌△CBE. 如图,在△ABC中,D是BC上一点,∠1=∠2,∠BAC=68°,∠3=70°,求∠4的度数.
如图,在△ABC中,D是BC上一点,∠1=∠2,∠BAC=68°,∠3=70°,求∠4的度数.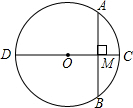 已知:如图,CD为⊙O的直径,AB为⊙O的弦.CD⊥AB,垂足为M,求证:AC=BC.
已知:如图,CD为⊙O的直径,AB为⊙O的弦.CD⊥AB,垂足为M,求证:AC=BC. 如图,∠AOD=∠BOD=∠COE=90°.找出图中互补和互余的角,和∠BOE相等的角是哪个?
如图,∠AOD=∠BOD=∠COE=90°.找出图中互补和互余的角,和∠BOE相等的角是哪个? 如图,⊙O内,弧AB等于弧CD,BP=5,求PD?
如图,⊙O内,弧AB等于弧CD,BP=5,求PD? 如图9个方格中,每行、每列、每条对角线上的三个数的和都相等.那么,右上角的数为2011.
如图9个方格中,每行、每列、每条对角线上的三个数的和都相等.那么,右上角的数为2011.