题目内容
10.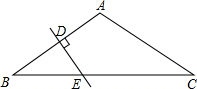 如图,在△ABC中,∠A=120°,AB=AC,AB的垂直平分线DE与AB,BC分别交于点D和E.若BE=3,试求CE的长.
如图,在△ABC中,∠A=120°,AB=AC,AB的垂直平分线DE与AB,BC分别交于点D和E.若BE=3,试求CE的长.
分析 如图,连接AE,根据线段的垂直平分线的性质得到AE=BE,而AB=AC,∠A=120°,根据等腰三角形的性质得到∠B=∠C=∠BAE=30°,接着根据三角形的外角和内角的关系可以求出∠AEC,然后可以求出以∠EAC=90°,最后根据30°的角所对的直角边等于斜边的一半即可求出CE
解答 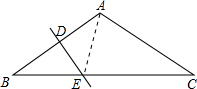 解:如图,连接AE.
解:如图,连接AE.
∵△ABC中,AB=AC,∠A=120°,
∴∠B=∠C=30°,
又∵AB的垂直平分线DE分别交AB、BC于D、E,
∴AE=BE=3,
∴∠B=∠BAE=30°,
∴∠AEC=∠B+∠BAE=60°,
∴∠EAC=180°-∠C-∠AEC=90°,
而AE=3,
∴CE=6.
点评 本题考查了线段垂直平分线的定义,等腰三角形的性质,勾股定理的应用,以及直角三角形30°角所对的直角边等于斜边的一半的性质,熟记性质是解题的关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
19.下列方程与方程2x2-x-2=0同解的是( )
| A. | (x-$\frac{1}{2}$)2=$\frac{5}{4}$ | B. | (x-$\frac{1}{2}$)2=$\frac{1}{4}$ | C. | (x-$\frac{1}{4}$)2=$\frac{9}{16}$ | D. | (x-$\frac{1}{4}$)2=$\frac{17}{16}$ |
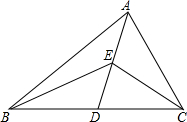 如图,在△ABC中,AD是中线,E是AD的中点,若△ABC的面积是24cm2,则△EBC的面积是12cm2.
如图,在△ABC中,AD是中线,E是AD的中点,若△ABC的面积是24cm2,则△EBC的面积是12cm2.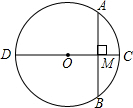 已知:如图,CD为⊙O的直径,AB为⊙O的弦.CD⊥AB,垂足为M,求证:AC=BC.
已知:如图,CD为⊙O的直径,AB为⊙O的弦.CD⊥AB,垂足为M,求证:AC=BC.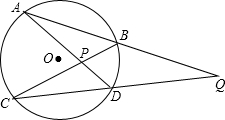 如图,⊙O的弦AB,CD的延长线相交于点Q,AD,CB相交于点P,试探索∠APC及∠Q的度数分别与$\widehat{AC}$和$\widehat{BD}$的度数有怎样的关系,并证明你的结论.
如图,⊙O的弦AB,CD的延长线相交于点Q,AD,CB相交于点P,试探索∠APC及∠Q的度数分别与$\widehat{AC}$和$\widehat{BD}$的度数有怎样的关系,并证明你的结论. 如图,⊙O内,弧AB等于弧CD,BP=5,求PD?
如图,⊙O内,弧AB等于弧CD,BP=5,求PD?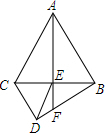 如图所示,△ACB,△ECD是等边三角形,且E点在BC上,AE的延长线交DB于F点,请你在图中找出一对全等三角形,并写出证明它们全等的过程.
如图所示,△ACB,△ECD是等边三角形,且E点在BC上,AE的延长线交DB于F点,请你在图中找出一对全等三角形,并写出证明它们全等的过程.
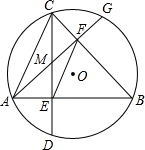 如图,在⊙O中,弦AB⊥弦CD于E,弦AG⊥弦BC于F点,CD与AG相交于M点.
如图,在⊙O中,弦AB⊥弦CD于E,弦AG⊥弦BC于F点,CD与AG相交于M点.