题目内容
7.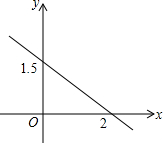 根据所给的函数图象.求出相应的函数关系式.
根据所给的函数图象.求出相应的函数关系式.
分析 设一次函数的关系式为y=mx+n,由图象可知直线与x轴、y轴的交点坐标分别为(2,0),(0,1.5),把两点坐标分别代入一次函数关系式即可的方程组;解可得m、n的值即可.
解答 解:由图象可知直线与x轴、y轴的交点坐标分别为(2,0),(0,1.5),
设一次函数的关系式为y=mx+n,把两点坐标分别得$\left\{\begin{array}{l}{2m+n=0}\\{n=1.5}\end{array}\right.$;
解得$\left\{\begin{array}{l}{m=-\frac{3}{4}}\\{n=1.5}\end{array}\right.$;
故直线的解析式为:y=-$\frac{3}{4}$x+1.5.
点评 本题主要考查待定系数法求一次函数解析式,熟练掌握待定系数法是解题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
16.方程ax+1=3的解是x=-2,则a的值是( )
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
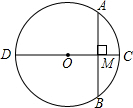 已知:如图,CD为⊙O的直径,AB为⊙O的弦.CD⊥AB,垂足为M,求证:AC=BC.
已知:如图,CD为⊙O的直径,AB为⊙O的弦.CD⊥AB,垂足为M,求证:AC=BC. 如图,⊙O内,弧AB等于弧CD,BP=5,求PD?
如图,⊙O内,弧AB等于弧CD,BP=5,求PD?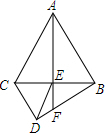 如图所示,△ACB,△ECD是等边三角形,且E点在BC上,AE的延长线交DB于F点,请你在图中找出一对全等三角形,并写出证明它们全等的过程.
如图所示,△ACB,△ECD是等边三角形,且E点在BC上,AE的延长线交DB于F点,请你在图中找出一对全等三角形,并写出证明它们全等的过程.