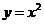 引导学生用列表描点法,应用函数的性质,如奇偶性,定义域等,画出函数图像,最后,教师利用电脑软件画出以上五个数数的图像.
引导学生用列表描点法,应用函数的性质,如奇偶性,定义域等,画出函数图像,最后,教师利用电脑软件画出以上五个数数的图像.
|
|
|

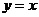
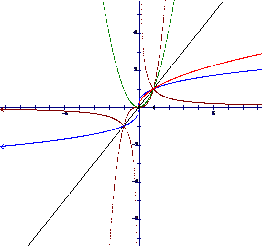
让学生通过观察图像,分组讨论,探究幂函数的性质和图像的变化规律,教师注意引导学生用类比研究指数函数,对函数的方法研究幂函数的性质.
通过观察图像,填P91探究中的表格
|
|
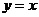 |
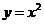 |
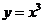 |
 |
 |
|
定义域 |
R |
R |
R |
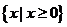 |
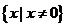 |
|
奇偶性 |
奇 |
奇 |
奇 |
非奇非偶 |
奇 |
|
在第Ⅰ象限单调增减性 |
在第Ⅰ象限单调递增 |
在第Ⅰ象限单调递增 |
在第Ⅰ象限单调递增 |
在第Ⅰ象限单调递增 |
在第Ⅰ象限单调递减 |
|
定点 |
(1,1) |
(1,1) |
(1,1) |
(1,1) |
(1,1) |
3.幂函数性质
(1)所有的幂函数在(0,+∞)都有定义,并且图象都过点(1,1)(原因: );
);
(2) >0时,幂函数的图象都通过原点,并且在[0,+∞]上,是增函数(从左往右看,函数图象逐渐上升).
>0时,幂函数的图象都通过原点,并且在[0,+∞]上,是增函数(从左往右看,函数图象逐渐上升).
特别地,当 >1,
>1, >1时,
>1时, ∈(0,1),
∈(0,1),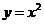 的图象都在
的图象都在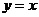 图象的下方,形状向下凸越大,下凸的程度越大(你能找出原因吗?)
图象的下方,形状向下凸越大,下凸的程度越大(你能找出原因吗?)
当∠α<1时, ∈(0,1),
∈(0,1),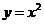 的图象都在
的图象都在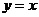 的图象上方,形状向上凸,α越小,上凸的程度越大(你能说出原因吗?)
的图象上方,形状向上凸,α越小,上凸的程度越大(你能说出原因吗?)
(3)α<0时,幂函数的图象在区间(0,+∞)上是减函数.
在第一家限内,当 向原点靠近时,图象在
向原点靠近时,图象在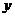 轴的右方无限逼近
轴的右方无限逼近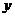 轴正半轴,当
轴正半轴,当 慢慢地变大时,图象在
慢慢地变大时,图象在 轴上方并无限逼近
轴上方并无限逼近 轴的正半轴.
轴的正半轴.
例题:
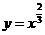 的大致图象,并求出其定义域、奇偶性,并判断和证明其单调性.
的大致图象,并求出其定义域、奇偶性,并判断和证明其单调性.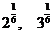 (2)
(2)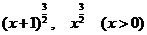 (3)
(3)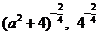
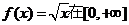 上是增函数
上是增函数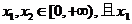 <
<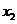 则
则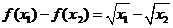
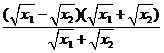
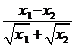
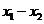 <0,
<0,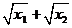 >0
>0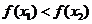 ,即
,即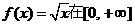 上是增函数.
上是增函数.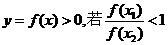 得
得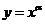 (
( R)的函数称为幂孙函数,其中
R)的函数称为幂孙函数,其中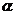 是常数.
是常数.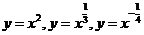 等都是幂函数,幂函数与指数函数,对数函数一样,都是基本初等函数.
等都是幂函数,幂函数与指数函数,对数函数一样,都是基本初等函数.