摘要:2.研究函数的图像 (1) (2) (3) (4) (5)
网址:http://m.1010jiajiao.com/timu_id_4460304[举报]
研究函数的对称中心有如下结论:如果存在实数a, b使![]() 恒成立,则(a, b)为函数
恒成立,则(a, b)为函数![]() 的图像的对称中心.
的图像的对称中心.
(1)求证函数![]() 的图像的对称中心为(0,1),并求函数
的图像的对称中心为(0,1),并求函数![]() 的图象的对称中心;
的图象的对称中心;
(2)试用函数的性质及图象变换解释:“如果存在实数a, b使![]() 恒成立,则(a, b)为函数
恒成立,则(a, b)为函数![]() 的图象的对称中心.”
的图象的对称中心.”
(3)是否存在函数![]() ,使函数
,使函数![]() 的图象有相同的对称中心(c,d)?请对
的图象有相同的对称中心(c,d)?请对![]() 时,说明你的结论与理由.
时,说明你的结论与理由.
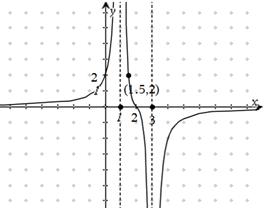
已知函数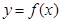 的图像(如图所示)过点
的图像(如图所示)过点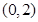 、
、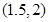 和点
和点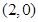 ,且函数图像关于点
,且函数图像关于点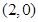 对称;直线
对称;直线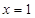 和
和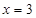 及
及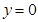 是它的渐近线.现要求根据给出的函数图像研究函数
是它的渐近线.现要求根据给出的函数图像研究函数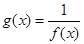 的相关性质与图像,
的相关性质与图像,
(1)写出函数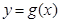 的定义域、值域及单调递增区间;
的定义域、值域及单调递增区间;
(2)作函数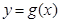 的大致图像(要充分反映由图像及条件给出的信息);
的大致图像(要充分反映由图像及条件给出的信息);
(3)试写出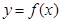 的一个解析式,并简述选择这个式子的理由(按给出理由的完整性及表达式的合理、简洁程度分层给分
的一个解析式,并简述选择这个式子的理由(按给出理由的完整性及表达式的合理、简洁程度分层给分
查看习题详情和答案>>
已知函数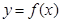 的图像(如图所示)过点
的图像(如图所示)过点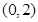 、
、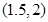 和点
和点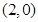 ,且函数图像关于点
,且函数图像关于点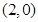 对称;直线
对称;直线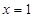 和
和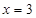 及
及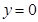 是它的渐近线.现要求根据给出的函数图像研究函数
是它的渐近线.现要求根据给出的函数图像研究函数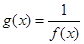 的相关性质与图像,
的相关性质与图像,
(1)写出函数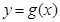 的定义域、值域及单调递增区间;
的定义域、值域及单调递增区间;
(2)作函数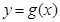 的大致图像(要充分反映由图像及条件给出的信息);
的大致图像(要充分反映由图像及条件给出的信息);
(3)试写出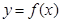 的一个解析式,并简述选择这个式子的理由(按给出理由的完整性及表达式的合理、简洁程度分层给分
的一个解析式,并简述选择这个式子的理由(按给出理由的完整性及表达式的合理、简洁程度分层给分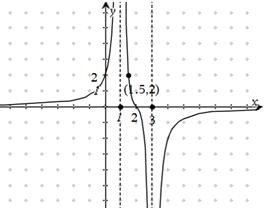
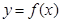 的图像(如图所示)过点
的图像(如图所示)过点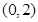 、
、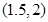 和点
和点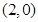 ,且函数图像关于点
,且函数图像关于点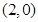 对称;直线
对称;直线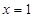 和
和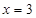 及
及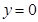 是它的渐近线.现要求根据给出的函数图像研究函数
是它的渐近线.现要求根据给出的函数图像研究函数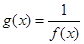 的相关性质与图像,
的相关性质与图像,(1)写出函数
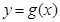 的定义域、值域及单调递增区间;
的定义域、值域及单调递增区间;(2)作函数
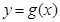 的大致图像(要充分反映由图像及条件给出的信息);
的大致图像(要充分反映由图像及条件给出的信息);(3)试写出
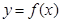 的一个解析式,并简述选择这个式子的理由(按给出理由的完整性及表达式的合理、简洁程度分层给分
的一个解析式,并简述选择这个式子的理由(按给出理由的完整性及表达式的合理、简洁程度分层给分
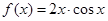 的性质进行研究,得出如下的结论:
的性质进行研究,得出如下的结论:  在
在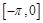 上单调递增,在
上单调递增,在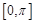 上单调递减;
上单调递减;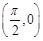 是函数
是函数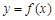 图像的一个对称中心;
图像的一个对称中心;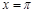 对称;
对称;  ,使
,使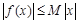 对一切实数
对一切实数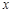 均成立.
均成立.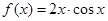 的性质进行研究,得出如下的结论:
的性质进行研究,得出如下的结论: 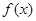 在
在 上单调递增,在
上单调递增,在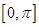 上单调递减;
上单调递减;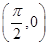 是函数
是函数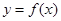 图像的一个对称中心;
图像的一个对称中心;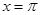 对称;
对称;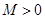 ,使
,使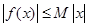 对一切实数
对一切实数 均成立.其中正确的结论是
.
均成立.其中正确的结论是
.