(三)质疑答辩,排难解惑,发展思维.
例1.某种笔记本的单价是5元,买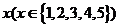 个笔记本需要
个笔记本需要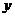 元,试用三种表示法表示函数
元,试用三种表示法表示函数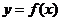 .
.
分析:注意本例的设问,此处“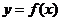 ”有三种含义,它可以是解析表达式,可以是图象,也可以是对应值表.
”有三种含义,它可以是解析表达式,可以是图象,也可以是对应值表.
解:(略)
注意:
①函数图象既可以是连续的曲线,也可以是直线、折线、离散的点等等;
②解析法:必须注明函数的定义域;
③图象法:是否连线;
④列表法:选取的自变量要有代表性,应能反映定义域的特征.
例2.下表是某校高一(1)班三位同学在高一学年度几次数学测试的成绩及班级平均分表:
|
|
第一次 |
第二次 |
第三次 |
第四次 |
第五次 |
第六次 |
|
王
伟 |
98 |
87 |
91 |
92 |
88 |
95 |
|
张
城 |
90 |
76 |
88 |
75 |
86 |
80 |
|
赵
磊 |
68 |
65 |
73 |
72 |
75 |
82 |
|
班平均分 |
88.2 |
78.3 |
85.4 |
80.3 |
75.7 |
82.6 |
请你对这三位同学在高一学年度的数学学习情况做一个分析.
分析:本例应引导学生分析题目要求,做学情分析,具体要分析什么?怎么分析?借助什么工具?
解:(略)
注意:
①本例为了研究学生的学习情况,将离散的点用虚线连接,这样更便于研究成绩的变化特点:
②本例能否用解析法?为什么?
例3.画出函数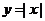 的图象
的图象
解:(略)
例4.某市郊空调公共汽车的票价按下列规则制定:
(1)乘坐汽车5公里以内,票价2元;
(2)5公里以上,每增加5公里,票价增加1元(不足5公里按5公里计算),已知两个相邻的公共汽车站间相距约为1公里,如果沿途(包括起点站和终点站)设20个汽车站,请根据题意,写出票价与里程之间的函数解析式,并画出函数的图象.
分析:本例是一个实际问题,有具体的实际意义,根据实际情况公共汽车到站才能停车,所以行车里程只能取整数值.
解:(略)
注意:
①本例具有实际背景,所以解题时应考虑其实际意义;
②象例3、例4中的函数,称为分段函数.
③分段函数的解析式不能写成几个不同的方程,而就写函数值几种不同的表达式并用一个左大括号括起来,并分别注明各部分的自变量的取值情况.
 ,面积为
,面积为
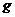 ,付邮资80分,超过20
,付邮资80分,超过20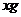 (0<
(0<