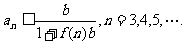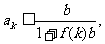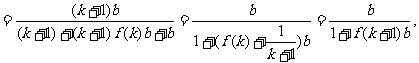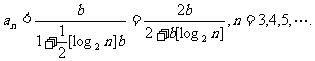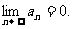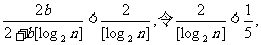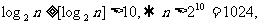1.(本小题满分14分)
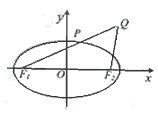
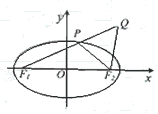
已知椭圆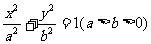 的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的动点,满足
的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的动点,满足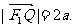 点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足
点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足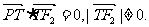
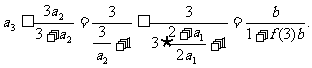
 (Ⅰ)设
(Ⅰ)设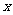 为点P的横坐标,证明
为点P的横坐标,证明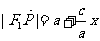 ;
;
(Ⅱ)求点T的轨迹C的方程;
(Ⅲ)试问:在点T的轨迹C上,是否存在点M,
使△F1MF2的面积S=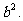 若存在,求∠F1MF2
若存在,求∠F1MF2
的正切值;若不存在,请说明理由.
本小题主要考查平面向量的概率,椭圆的定义、标准方程和有关性质,轨迹的求法和应用,以及综合运用数学知识解决问题的能力.满分14分.
 (Ⅰ)证法一:设点P的坐标为
(Ⅰ)证法一:设点P的坐标为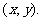
由P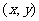 在椭圆上,得
在椭圆上,得
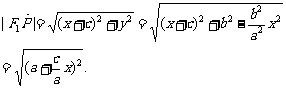
由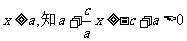 ,所以
,所以 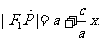 ………………………3分
………………………3分
证法二:设点P的坐标为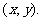 记
记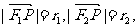
则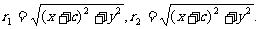
由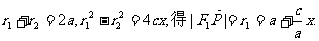
证法三:设点P的坐标为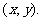 椭圆的左准线方程为
椭圆的左准线方程为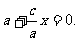
由椭圆第二定义得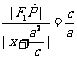 ,即
,即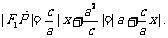
由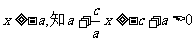 ,所以
,所以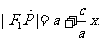 …………………………3分
…………………………3分
(Ⅱ)解法一:设点T的坐标为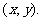
当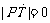 时,点(
时,点(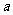 ,0)和点(-
,0)和点(-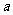 ,0)在轨迹上.
,0)在轨迹上.
当| 时,由
时,由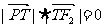 ,得
,得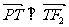 .
.
又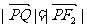 ,所以T为线段F2Q的中点.
,所以T为线段F2Q的中点.
在△QF1F2中,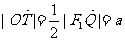 ,所以有
,所以有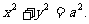
综上所述,点T的轨迹C的方程是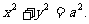 …………………………7分
…………………………7分
解法二:设点T的坐标为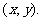 当
当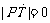 时,点(
时,点(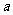 ,0)和点(-
,0)和点(-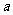 ,0)在轨迹上.
,0)在轨迹上.
当| 时,由
时,由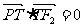 ,得
,得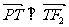 .
.
又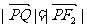 ,所以T为线段F2Q的中点.
,所以T为线段F2Q的中点.
设点Q的坐标为(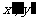 ),则
),则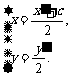
因此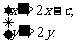 ①
①
由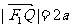 得
得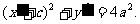 ②
②
将①代入②,可得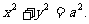
综上所述,点T的轨迹C的方程是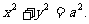 ……………………7分
……………………7分
|
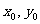 )使S=
)使S=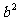 的充要条件是
的充要条件是
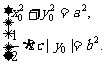
由③得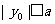 ,由④得
,由④得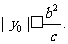 所以,当
所以,当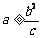 时,存在点M,使S=
时,存在点M,使S=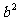 ;
;
当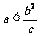 时,不存在满足条件的点M.………………………11分
时,不存在满足条件的点M.………………………11分
当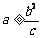 时,
时,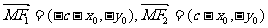 ,
,
由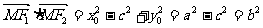 ,
,
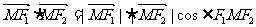 ,
,
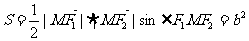 ,得
,得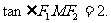
解法二:C上存在点M(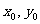 )使S=
)使S=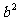 的充要条件是
的充要条件是
|
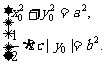
由④得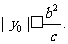 上式代入③得
上式代入③得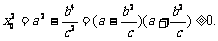
于是,当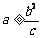 时,存在点M,使S=
时,存在点M,使S=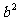 ;
;
当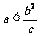 时,不存在满足条件的点M.………………………11分
时,不存在满足条件的点M.………………………11分
当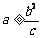 时,记
时,记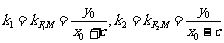 ,
,
由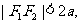 知
知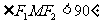 ,所以
,所以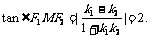 …………14分
…………14分
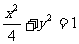 ,双曲线C2的左、右焦点分别为C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点.
,双曲线C2的左、右焦点分别为C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点.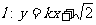 与椭圆C1及双曲线C2都恒有两个不同的交点,且l与C2的两个交点A和B满足
与椭圆C1及双曲线C2都恒有两个不同的交点,且l与C2的两个交点A和B满足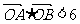 (其中O为原点),求k的取值范围.
(其中O为原点),求k的取值范围.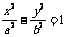 ,则
,则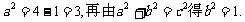
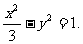

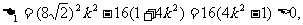
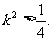 ①
①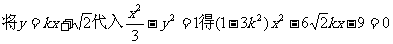 .
.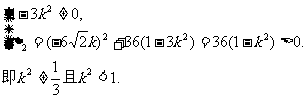
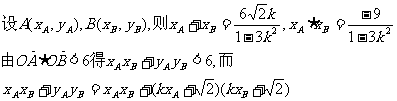
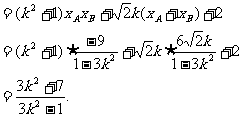
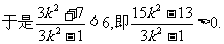 解此不等式得
解此不等式得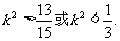 ③
③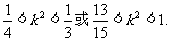
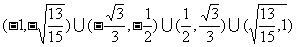
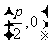 ,且与直线
,且与直线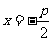 相切,其中
相切,其中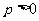 .
.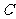 的轨迹的方程;
的轨迹的方程;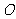 的两个不同点,直线
的两个不同点,直线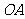 和
和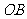 的倾斜角分别为
的倾斜角分别为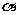 和
和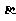 ,当
,当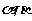 变化且
变化且 为定值
为定值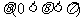 时,证明直线
时,证明直线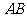 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标. 为动圆圆心,
为动圆圆心, ,过点
,过点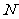 ,由题意知:
,由题意知: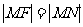 即动点
即动点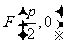 为焦点,
为焦点,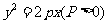 ;
;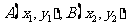 ,由题意得
,由题意得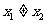 (否则
(否则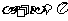 )且
)且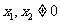 所以直线
所以直线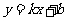 ,显然
,显然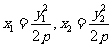 ,将
,将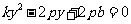 由韦达定理知
由韦达定理知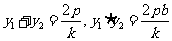 ①
①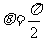 时,即
时,即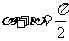 时,
时, 所以
所以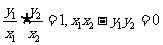 ,
,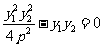 所以
所以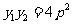 由①知:
由①知: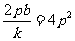 所以
所以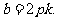 因此直线
因此直线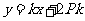 ,即
,即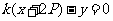 所以直线
所以直线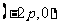
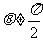 时,由
时,由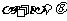 ,得
,得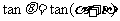 =
=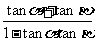 =
=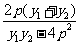 将①式代入上式整理化简可得:
将①式代入上式整理化简可得: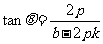 ,所以
,所以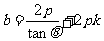 ,
,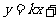
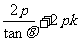 即
即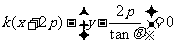
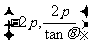
 的首项
的首项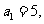 前
前 项和为
项和为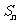 ,且
,且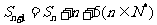
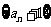 是等比数列;
是等比数列;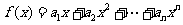 ,求函数
,求函数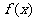 在点
在点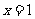 处的导数
处的导数 并比较
并比较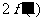 与
与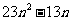 的大小.
的大小.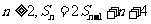 两式相减得
两式相减得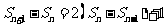 即
即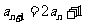 从而
从而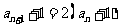 当
当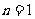 时
时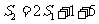 所以
所以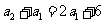 又
又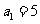 所以
所以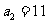 从而
从而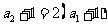
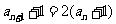 ,
,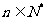 又
又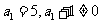 从而
从而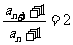 即数列
即数列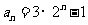
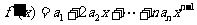
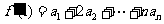 =
=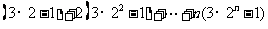
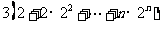 -
-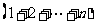 =
=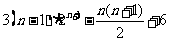
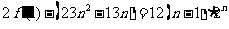 -
-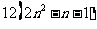 =
=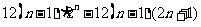 =12
=12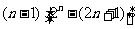 ①
①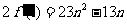 ;
;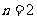 时,①式=-12
时,①式=-12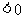 所以
所以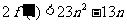
 当
当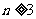 时,
时,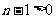
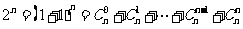

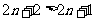
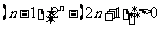 即①
即① 从而
从而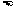
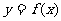 在区间(0,+∞)内可导,导函数
在区间(0,+∞)内可导,导函数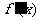 是减函数,且
是减函数,且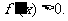 设
设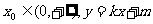 是曲线
是曲线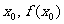 )得的切线方程,并设函数
)得的切线方程,并设函数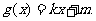
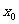 、
、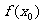 、
、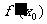 表示m;
表示m;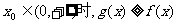 ;
;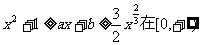 上恒成立,其中a、b为实数,
上恒成立,其中a、b为实数,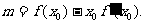 …………………………………………2分
…………………………………………2分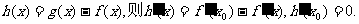
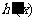 递增,因此,当
递增,因此,当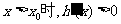 ;
;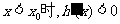 .所以
.所以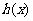 唯一的极值点,且是极小值点,可知
唯一的极值点,且是极小值点,可知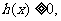 即
即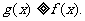 …………………………6分
…………………………6分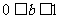 ,
, 是不等式成立的必要条件,以下讨论设此条件成立.
是不等式成立的必要条件,以下讨论设此条件成立.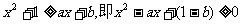 对任意
对任意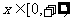 成立的充要条件是
成立的充要条件是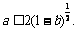
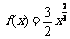 满足前述题设中关于函数
满足前述题设中关于函数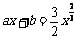 的充要条件是:过点(0,
的充要条件是:过点(0,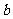 )与曲线
)与曲线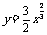 相切的直线的斜率大于
相切的直线的斜率大于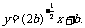
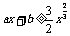 的充要条件是
的充要条件是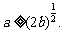 …………………………10分
…………………………10分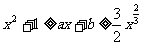 对任意
对任意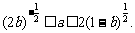 ①
①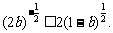 ②
②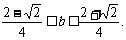 ③
③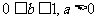 是不等式成立的必要条件,以下讨论设此条件成立.
是不等式成立的必要条件,以下讨论设此条件成立.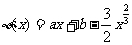 ,于是
,于是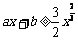 对任意
对任意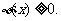 由
由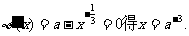
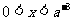 时
时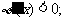 当
当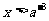 时,
时,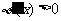 ,所以,当
,所以,当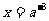 时,
时,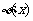 取最小值.因此
取最小值.因此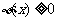 成立的充要条件是
成立的充要条件是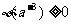 ,即
,即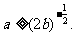 ………………10分
………………10分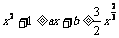 对任意
对任意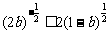 ②
②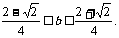
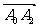 的坐标;
的坐标;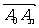 的坐标.
的坐标.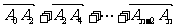 ,
,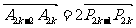 ,得
,得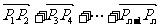 )=2({1,2}+{1,23}+┄+{1,2n-1})=2{
)=2({1,2}+{1,23}+┄+{1,2n-1})=2{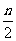 ,
,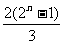 }={n,
}={n,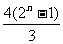 }
} f(x)·g(x) 当x∈Df且x∈Dg
f(x)·g(x) 当x∈Df且x∈Dg Dg
Dg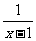 ,g(x)=x2,x∈R,写出函数h(x)的解析式;
,g(x)=x2,x∈R,写出函数h(x)的解析式;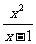 x∈(-∞,1)∪(1,+∞)
x∈(-∞,1)∪(1,+∞)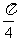
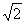 sin2x, α=
sin2x, α=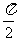 ,
,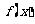 和
和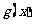 的图象关于原点对称,且
的图象关于原点对称,且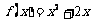 .
.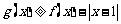 ;
;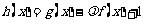 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围.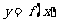 的图象上任意一点
的图象上任意一点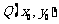 关于原点的对称点为
关于原点的对称点为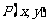 ,则
,则
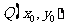 在函数
在函数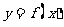 的图象上
的图象上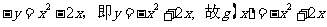
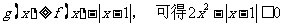
 时,
时,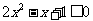 ,此时不等式无解.
,此时不等式无解.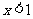 时,
时,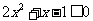 ,解得
,解得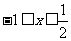 .
.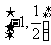 .
.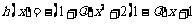
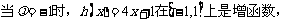
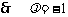
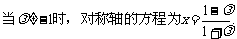

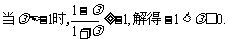
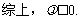
 (Ⅰ)求椭圆的方程;
(Ⅰ)求椭圆的方程;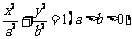 ,半焦距为
,半焦距为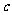 ,则
,则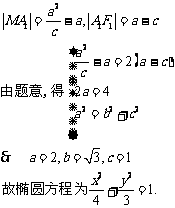

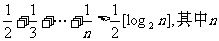 为大于2的整数,
为大于2的整数,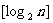 表示不超过
表示不超过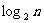 的最大整数. 设数列
的最大整数. 设数列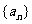 的各项为正,且满足
的各项为正,且满足
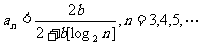
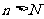 时,对任意b>0,都有
时,对任意b>0,都有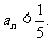
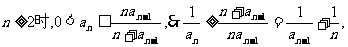
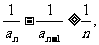
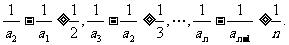
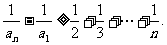
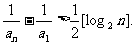
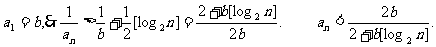
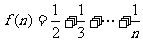 ,首先利用数学归纳法证不等式
,首先利用数学归纳法证不等式