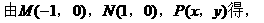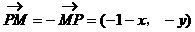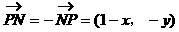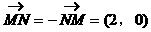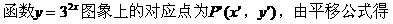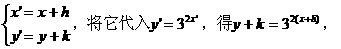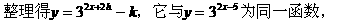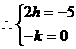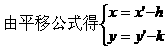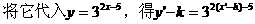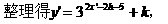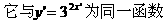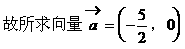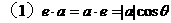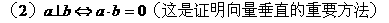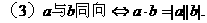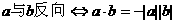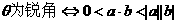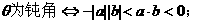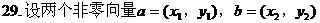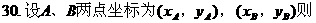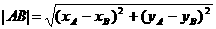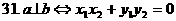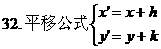0 52629 52637 52643 52647 52653 52655 52659 52665 52667 52673 52679 52683 52685 52689 52695 52697 52703 52707 52709 52713 52715 52719 52721 52723 52724 52725 52727 52728 52729 52731 52733 52737 52739 52743 52745 52749 52755 52757 52763 52767 52769 52773 52779 52785 52787 52793 52797 52799 52805 52809 52815 52823 447348
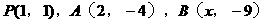 三点共线,则( )
三点共线,则( )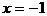 B.
B.
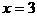
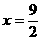 D.
D.
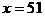
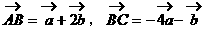 ,
,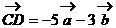 ,其中
,其中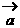 、
、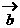 不共线,则四边形ABCD为( )
不共线,则四边形ABCD为( )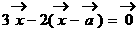 ,则向量
,则向量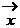 =( )
=( )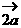 B.
B. 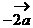 C.
C. 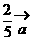 D.
D. 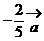
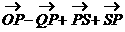 的结果是( )
的结果是( )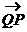 B.
B. 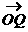 C.
C. 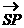 D.
D. 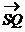
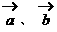 为非零向量,且
为非零向量,且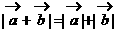 ,则( )
,则( )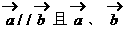 方向相同
方向相同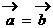
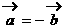
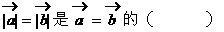
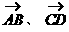 共线,则A、B、C、D四点必在同一直线上
共线,则A、B、C、D四点必在同一直线上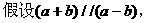
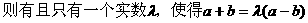
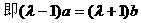
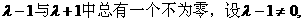
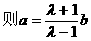
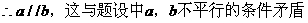
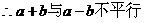
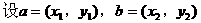
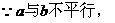
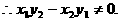
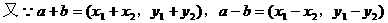
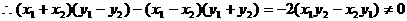
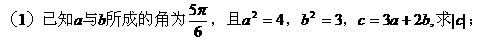


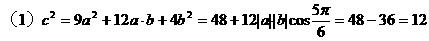
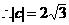
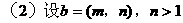

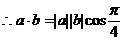
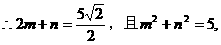
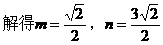
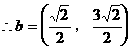

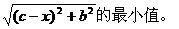
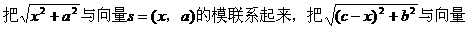
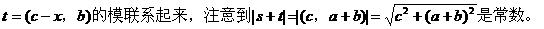
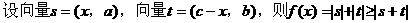
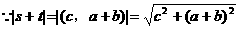
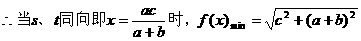
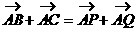

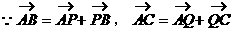
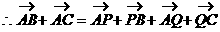
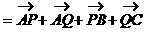
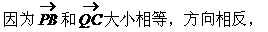
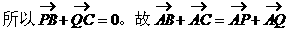
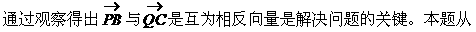

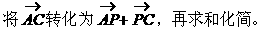
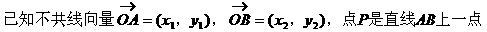
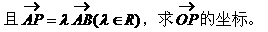
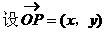
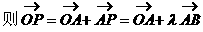
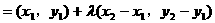
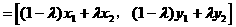
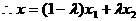
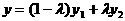

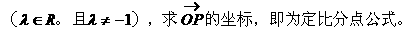
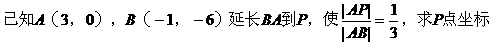
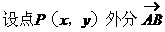
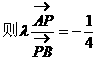
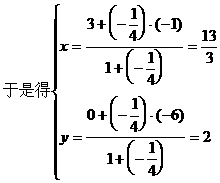
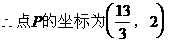
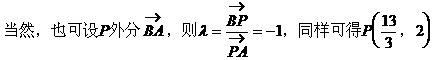
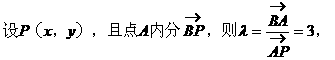
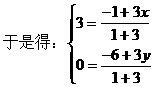
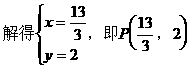
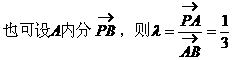
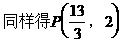

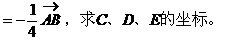
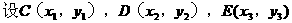
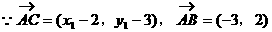
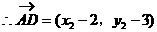
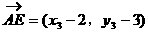
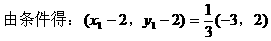
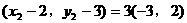
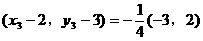
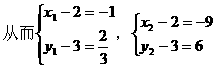
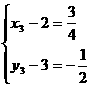
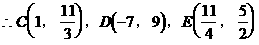
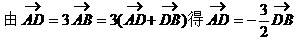
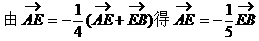
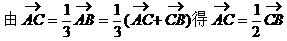
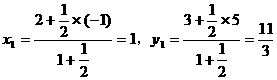
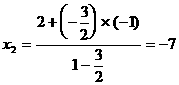
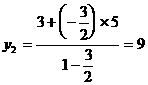
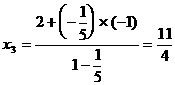
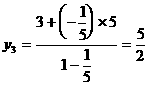
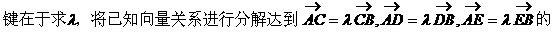 形式,从而分别求出λ。
形式,从而分别求出λ。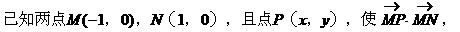
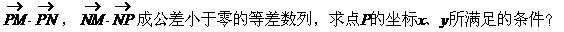 解:
解: