摘要:1. 已知椭圆的左.右焦点分别是F1.F2(c.0).Q是椭圆外的动点.满足点P是线段F1Q与该椭圆的交点.点T在线段F2Q上.并且满足 (Ⅰ)设为点P的横坐标.证明, (Ⅱ)求点T的轨迹C的方程, (Ⅲ)试问:在点T的轨迹C上.是否存在点M. 使△F1MF2的面积S=若存在.求∠F1MF2 的正切值,若不存在.请说明理由. 本小题主要考查平面向量的概率.椭圆的定义.标准方程和有关性质.轨迹的求法和应用.以及综合运用数学知识解决问题的能力.满分14分. (Ⅰ)证法一:设点P的坐标为 由P在椭圆上.得 由.所以 ---------3分 证法二:设点P的坐标为记 则 由 证法三:设点P的坐标为椭圆的左准线方程为 由椭圆第二定义得.即 由.所以----------3分 (Ⅱ)解法一:设点T的坐标为 当时.点(.0)和点(-.0)在轨迹上. 当|时.由.得. 又.所以T为线段F2Q的中点. 在△QF1F2中..所以有 综上所述.点T的轨迹C的方程是----------7分 解法二:设点T的坐标为 当时.点(.0)和点(-.0)在轨迹上. 当|时.由.得. 又.所以T为线段F2Q的中点. 设点Q的坐标为().则 因此 ① 由得 ② 将①代入②.可得 综上所述.点T的轨迹C的方程是--------7分 ③ ④ (Ⅲ)解法一:C上存在点M()使S=的充要条件是 由③得.由④得 所以.当时.存在点M.使S=, 当时.不存在满足条件的点M.---------11分 当时.. 由. . .得 解法二:C上存在点M()使S=的充要条件是 ③ ④ 由④得 上式代入③得 于是.当时.存在点M.使S=, 当时.不存在满足条件的点M.---------11分 当时.记. 由知.所以----14分
网址:http://m.1010jiajiao.com/timu3_id_528236[举报]
(本小题满分14分)
已知椭圆C:![]() ,左焦点
,左焦点![]() ,且离心率
,且离心率![]()
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线![]() 与椭圆C交于不同的两点
与椭圆C交于不同的两点![]() (
(![]() 不是左、右顶点),且以
不是左、右顶点),且以![]() 为直径的圆经过椭圆C的右顶点A. 求证:直线
为直径的圆经过椭圆C的右顶点A. 求证:直线![]() 过定点,并求出定点的坐标.
过定点,并求出定点的坐标.
(本小题满分14分)
已知椭圆C:![]() ,左焦点
,左焦点![]() ,且离心率
,且离心率![]()
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线![]() 与椭圆C交于不同的两点
与椭圆C交于不同的两点![]() (
(![]() 不是左、右顶点),且以
不是左、右顶点),且以![]() 为直径的圆经过椭圆C的右顶点A. 求证:直线
为直径的圆经过椭圆C的右顶点A. 求证:直线![]() 过定点,并求出定点的坐标.
过定点,并求出定点的坐标.
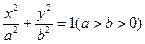 的左右焦点分别为
的左右焦点分别为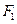 、
、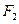 ,离心率
,离心率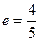 ,直线
,直线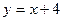 经过椭圆的左焦点
经过椭圆的左焦点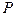 满足:
满足: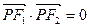 ,求
,求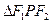 的面积.
的面积. (本小题满分14分)设b>0,椭圆方程为
(本小题满分14分)设b>0,椭圆方程为 的左、右焦点分别为F1、F2,若以F2为圆心,b-c为半径作圆F2,过椭圆上一点P作此圆的切线,切点为T,且
的左、右焦点分别为F1、F2,若以F2为圆心,b-c为半径作圆F2,过椭圆上一点P作此圆的切线,切点为T,且 的最小值不小于
的最小值不小于 。
。 ;
; 轴的右交点为Q,过点Q作斜率为
轴的右交点为Q,过点Q作斜率为 的直线
的直线 与椭圆相交于A、B两点,若OA⊥OB,求直线
与椭圆相交于A、B两点,若OA⊥OB,求直线