摘要:7.本题共有3个小题,第1小题满分4分, 第2小题满分8分, 第3小题满分6分. 在直角坐标平面中,已知点P1(1,2),P2(2,22),┄,Pn(n,2n),其中n是正整数.对平面上任一点A0,记A1为A0关于点P1的对称点, A2为A1关于点P2的对称点, ┄, AN为AN-1关于点PN的对称点. (1)求向量的坐标; (2)当点A0在曲线C上移动时, 点A2的轨迹是函数y=f是以3为周期的周期函数,且当x∈=lgx.求以曲线C为图象的函数在(1,4]上的解析式; (3)对任意偶数n,用n表示向量的坐标. [解](1)设点A0(x,y), A0为P1关于点的对称点A0的坐标为, A1为P2关于点的对称点A2的坐标为, ∴={2,4}. (2) ∵={2,4}, ∴f(x)的图象由曲线C向右平移2个单位,再向上平移4个单位得到. 因此, 曲线C是函数y=g是以3为周期的周期函数,且当x∈-4.于是,当x∈-4. 另解设点A0(x,y), A2(x2,y2),于是x2-x=2,y2-y=4, 若3< x2≤6,则0< x2-3≤3,于是f(x2)=f(x2-3)=lg(x2-3). 当1< x≤4时, 则3< x2≤6,y+4=lg(x-1). ∴当x∈-4. (3) =, 由于,得 =2()=2({1,2}+{1,23}+┄+{1,2n-1})=2{,}={n,}
网址:http://m.1010jiajiao.com/timu3_id_528235[举报]
(本大题满分18分)本大题共有3个小题,第1小题满分4分,第2小题满6分,第3小题满8分.
已知函数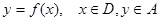 ;
;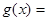
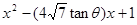 ,
,
(1)当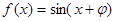 为偶函数时,求
为偶函数时,求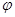 的值。
的值。
(2)当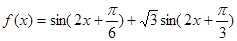 时,
时,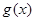 在
在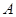 上是单调递增函数,求
上是单调递增函数,求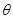 的取值范围。
的取值范围。
(3)当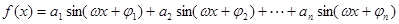 时,(其中
时,(其中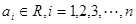 ,
,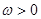 ),若
),若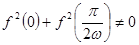 ,且函数
,且函数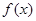 的图像关于点
的图像关于点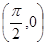 对称,在
对称,在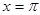 处取得最小值,试探讨
处取得最小值,试探讨 应该满足的条件。
应该满足的条件。
查看习题详情和答案>>
(本大题满分18分)本大题共有3个小题,第1小题满分4分,第2小题满6分,第3小题满8分.
已知集合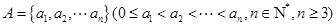 具有性质
具有性质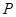 :对任意
:对任意 ,
,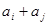 与
与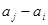 至少一个属于
至少一个属于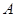 .
.
(1)分别判断集合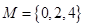 与
与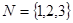 是否具有性质
是否具有性质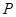 ,并说明理由;
,并说明理由;
(2)①求证: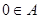 ;
;
②求证: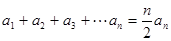 ;
;
(3)研究当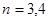 和
和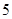 时,集合
时,集合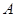 中的数列
中的数列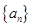 是否一定成等差数列.
是否一定成等差数列.
查看习题详情和答案>>
(本题共3小题,满分18分。第1小题满分4分,第2小题满分7分,第3小题7分)
对定义在 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数 称为
称为 函数.
函数.
① 对任意的 ,总有
,总有 ;
;
② 当 时,总有
时,总有 成立.
成立.
已知函数 与
与 是定义在
是定义在 上的函数.
上的函数.
(1)试问函数 是否为
是否为 函数?并说明理由;
函数?并说明理由;
(2)若函数 是
是 函数,求实数
函数,求实数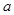 的值;
的值;
(3)在(2)的条件下,是否存在实数 ,使方程
,使方程 恰有两解?若存在,求出实数
恰有两解?若存在,求出实数 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看习题详情和答案>>
 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数 称为
称为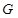 函数.
函数. ,总有
,总有 ;
; 时,总有
时,总有 成立.
成立. 与
与 是定义在
是定义在 是否为
是否为 函数?并说明理由;
函数?并说明理由; 是
是 的值;
的值; ,使方程
,使方程 恰有两解?若存在,求出实数
恰有两解?若存在,求出实数 ;
;
 ,
, 为偶函数时,求
为偶函数时,求 的值。
的值。 时,
时, 在
在 上是单调递增函数,求
上是单调递增函数,求 的取值范围。
的取值范围。 时,(其中
时,(其中 ,
, ),若
),若 ,且函数
,且函数 的图像关于点
的图像关于点 对称,在
对称,在 处取得最小值,试探讨
处取得最小值,试探讨 应该满足的条件。
应该满足的条件。