4.(广东21)(本小题满分14分)
设数列{an}满足a1=1,a2=2,an=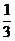 (an-1+2an-2)(n=3,4,…),数列{bn}满足b1=1,bn(n=2,3,…)是非零整数,且对任意的正整数m和自然数k,都有-1
(an-1+2an-2)(n=3,4,…),数列{bn}满足b1=1,bn(n=2,3,…)是非零整数,且对任意的正整数m和自然数k,都有-1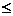 bm+bm+1+…+bm+1
bm+bm+1+…+bm+1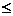 1.
1.
(1)求数列{an}和{bn}的通项公式;
(2) 记cn=nanbn(n=1,2,…),求数列{cn}的前n项和Sn.
解:(1)由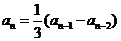 得
得 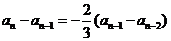
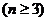
又  ,
,
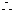 数列
数列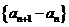 是首项为1公比为
是首项为1公比为 的等比数列,
的等比数列,

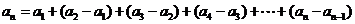
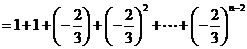
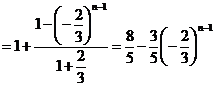 ,
,
由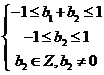 得
得
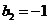 ,由
,由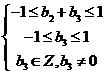 得
得
 ,…
,…
同理可得当n为偶数时,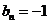 ;当n为奇数时,
;当n为奇数时,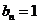 ;
;
|
|

|
|
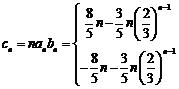
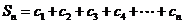
当n为奇数时,
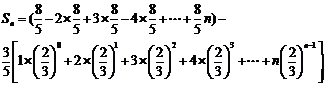
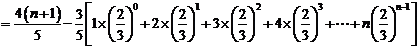
当n为偶数时,


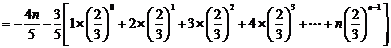
令 ……①
……①
①×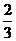 得:
得: 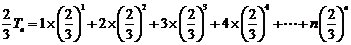 ……②
……②
①-②得: 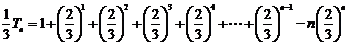
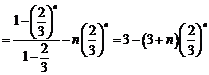
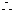
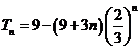
|
|
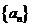 中的所有项按每一行比上一行多一项的规则排成如下数表:
中的所有项按每一行比上一行多一项的规则排成如下数表:

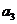
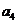
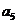
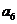
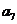

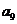
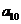
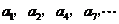 构成的数列为
构成的数列为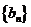 ,
,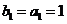 .
.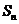 为数列
为数列 项和,且满足
项和,且满足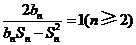 .
.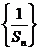 成等差数列,并求数列
成等差数列,并求数列 时,求上表中第
时,求上表中第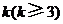 行所有项的和.
行所有项的和.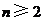 时,
时,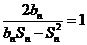 ,
,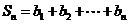 ,
,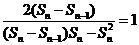 ,
,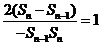 ,
,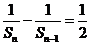 ,
,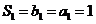 .
.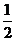 的等差数列.
的等差数列.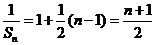 ,
, .
.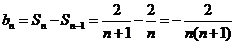 .
.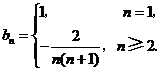
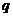 ,且
,且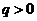 .
.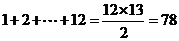 ,
, 在表中第13行第三列,
在表中第13行第三列,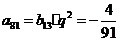 .
.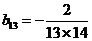 ,
,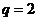 .
.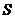 ,
, .
.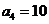 且
且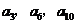 成等比数列,求数列
成等比数列,求数列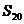 .
.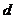 ,则
,则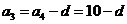 ,
,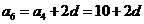 ,
,  .····························································································· 3分
.····························································································· 3分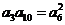 ,
,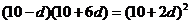 ,
,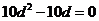 ,
, 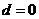 或
或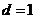 .····································································································· 7分
.····································································································· 7分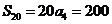 .·················································································· 9分
.·················································································· 9分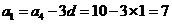 ,
,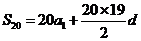
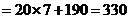 .······················································ 12分
.······················································ 12分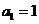 ,
,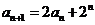 .
.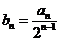 .证明:数列
.证明:数列 ,
,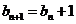 ,
,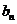 为等差数列,
为等差数列,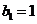 ,
,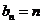 ,
,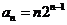 .
.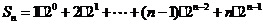
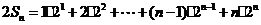
 .
.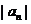 ,
,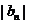 是各项均为正数的等比数列,设
是各项均为正数的等比数列,设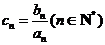 .
. 是否为等比数列?证明你的结论;
是否为等比数列?证明你的结论; ,
, 的前
的前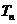 .若
.若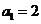 ,
,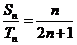 ,求数列
,求数列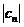 是等比数列.························································································· 2分
是等比数列.························································································· 2分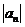 的公比为
的公比为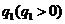 ,
,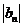 的公比为
的公比为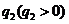 ,则
,则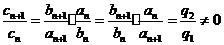 ,故
,故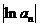 和
和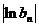 分别是公差为
分别是公差为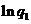 和
和 的等差数列.
的等差数列.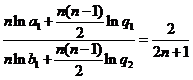 ,即
,即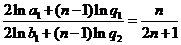 .····················································································· 7分
.····················································································· 7分 ,
,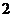 ,…,
,…,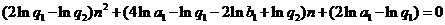 .
.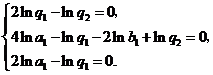
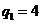 ,
,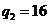 ,
,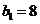 .································································· 10分
.································································· 10分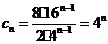 .
.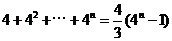 .······················································································ 12分
.······················································································ 12分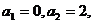
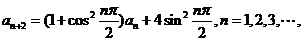
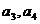 ,并求数列
,并求数列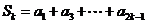 ,
,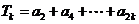 ,
,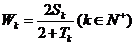 ,
,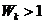 的所有k的值,并说明理由。
的所有k的值,并说明理由。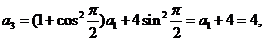
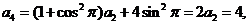 一般地, 当
一般地, 当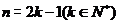 时,
时,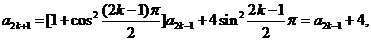
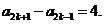 所以数列
所以数列 是首项为0、公差为4的等差数列,
是首项为0、公差为4的等差数列,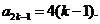
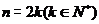 时,
时,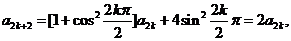
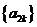 是首项为2、公比为2的等比数列,因此
是首项为2、公比为2的等比数列,因此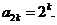
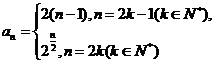
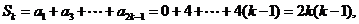
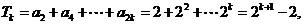
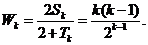
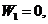
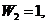
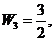
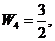

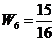 .
.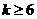 时,
时,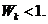 事实上, 当
事实上, 当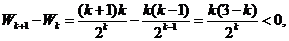 即
即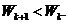
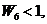 所以当
所以当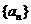 的各项均为正数,
的各项均为正数,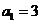 ,前
,前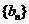 为等比数列,
为等比数列, 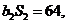
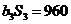 .
.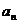 与
与 .
.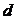 ,
,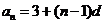 ,
,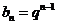
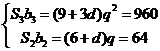 ①
①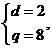 或
或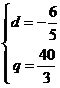 (舍去)
(舍去) 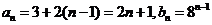
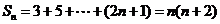
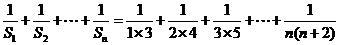
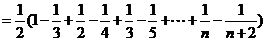
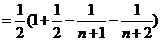
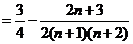
 是各项均不为零的等差数列(
是各项均不为零的等差数列(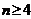 ),且公差
),且公差 ,若将此数列删去某一项得到的数列(按原来的顺序)是等比数列:
,若将此数列删去某一项得到的数列(按原来的顺序)是等比数列: 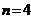 时,求
时,求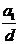 的数值;②求
的数值;②求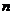 的所有可能值;
的所有可能值;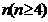 ,存在一个各项及公差都不为零的等差数列
,存在一个各项及公差都不为零的等差数列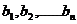 ,其中任意三项(按原来顺序)都不能组成等比数列。
,其中任意三项(按原来顺序)都不能组成等比数列。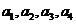 中不可能删去首项或末项,否则等差数列中连续三项成等比数列,则推出d=0。
中不可能删去首项或末项,否则等差数列中连续三项成等比数列,则推出d=0。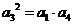 ,即
,即 化简得
化简得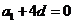 ,得
,得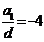
 ,即
,即 化简得
化简得 ,得
,得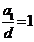
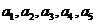 中同样不可能删去
中同样不可能删去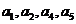 ,否则出现连续三项。
,否则出现连续三项。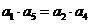 ,即
,即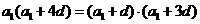 化简得
化简得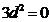 ,因为
,因为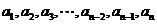 中,由于不能删去首项或末项,若删去
中,由于不能删去首项或末项,若删去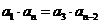 ,这与
,这与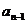 也有
也有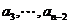 中任意一个,则必有
中任意一个,则必有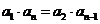 ,这与
,这与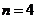 。
。 (
(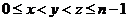 )为任意三项成等比数列,则
)为任意三项成等比数列,则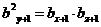 ,即
,即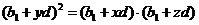 ,化简得
,化简得 (*)
(*)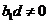 知,
知,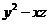 与
与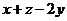 同时为0或同时不为0
同时为0或同时不为0 与题设矛盾。
与题设矛盾。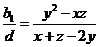
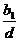 为有理数。
为有理数。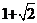 ,
,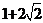 ,……,
,……,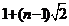 满足要求。
满足要求。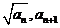 )(n
)(n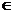 N*)在函数y=x2+1的图象上.
N*)在函数y=x2+1的图象上.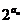 ,求证:bn ·bn+2<b2n+1.
,求证:bn ·bn+2<b2n+1.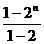 =2n-1.
=2n-1.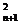 =(2n-1)(2n+2-1)-(2n-1-1)2
=(2n-1)(2n+2-1)-(2n-1-1)2 (
(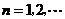 ),
),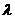 是常数.
是常数.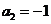 时,求
时,求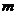 ,当
,当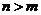 时总有
时总有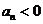 .
.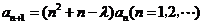 ,且
,且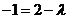 ,
,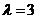 .
.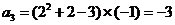 .
.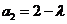 ,
, ,
,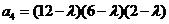 .
.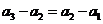 ,即
,即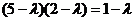 ,
,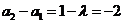 ,
, .
.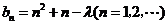 ,根据题意可知,
,根据题意可知,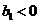 且
且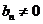 ,即
,即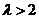 且
且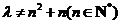 ,这时总存在
,这时总存在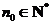 ,满足:当
,满足:当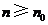 时,
时,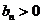 ;当
;当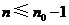 时,
时,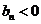 .
.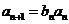 及
及 可知,若
可知,若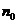 为偶数,则
为偶数,则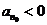 ,从而当
,从而当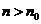 时,
时,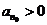 ,从而当
,从而当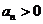 .
.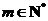 ,当
,当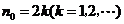 ,则
,则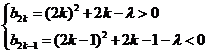 .
.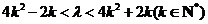 .
.