摘要:2. 数列满足.().是常数. (Ⅰ)当时.求及的值, (Ⅱ)数列是否可能为等差数列?若可能.求出它的通项公式,若不可能.说明理由, (Ⅲ)求的取值范围.使得存在正整数.当时总有. 解:(Ⅰ)由于.且. 所以当时.得. 故. 从而. (Ⅱ)数列不可能为等差数列.证明如下: 由.得 ... 若存在.使为等差数列.则.即. 解得. 于是.. 这与为等差数列矛盾.所以.对任意.都不可能是等差数列. (Ⅲ)记.根据题意可知.且.即且.这时总存在.满足:当时.,当时.. 所以由及可知.若为偶数.则.从而当时.,若为奇数.则.从而当时. 因此“存在.当时总有 的充分必要条件是:为偶数. 记.则满足 . 故的取值范围是.
网址:http://m.1010jiajiao.com/timu3_id_528011[举报]
(本小题满分13分 )对于给定数列
)对于给定数列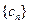 ,如果存在实常数
,如果存在实常数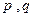 使得
使得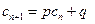 对于任意
对于任意 都成立,我们称数列
都成立,我们称数列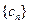 是 “M类数列”.
是 “M类数列”.
(1)若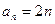 ,
,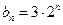 (
( ),数列
),数列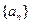 、
、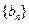 是否为“M类数列”?若是,指出它对应的实
是否为“M类数列”?若是,指出它对应的实 常数
常数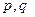 ,若不是,请说明理由;
,若不是,请说明理由;
(2)证明:若数列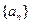 是“M类数
是“M类数 列”,则数列
列”,则数列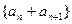 也是“M类数列”;
也是“M类数列”;
(3)若数列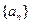 满足
满足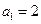 ,
,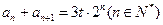 ,
,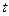 为常数,求数列
为常数,求数列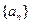 前
前 项的和,并判断
项的和,并判断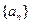 是否为“M类数列”,说明理由.
是否为“M类数列”,说明理由.
若数列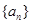 满足
满足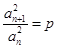 (
( 为正常数,
为正常数,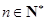 ),则称
),则称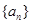 为“等方比数列”.
为“等方比数列”.
甲:数列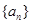 是等方比数列; 乙:数列
是等方比数列; 乙:数列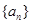 是等比数列,则( )
是等比数列,则( )
A.甲是乙的充分条件但不是必要条件
B.甲是乙的必要条件但不是充分条件
C.甲是乙的充要条件
D.甲既不是乙的充分条件也不是乙的必要条件
查看习题详情和答案>>
(07年湖北卷理)若数列![]() 满足
满足![]() (
(![]() 为正常数,
为正常数,![]() ),则称
),则称![]() 为“等方比数列”.
为“等方比数列”.
甲:数列![]() 是等方比数列;乙:数列
是等方比数列;乙:数列![]() 是等比数列,则( )
是等比数列,则( )
A.甲是乙的充分条件但不是必要条件
B.甲是乙的必要条件但不是充分条件
C.甲是乙的充要条件
D.甲既不是乙的充分条件也不是乙的必要条件
查看习题详情和答案>>(本题满分13分)
对于给定数列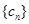 ,如果存在实常数
,如果存在实常数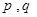 使得
使得 对于任意
对于任意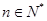 都成立,我们称数列
都成立,我们称数列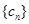 是 “M类数列”.
是 “M类数列”.
(1)若 ,
, ,
,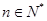 ,数列
,数列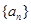 、
、 是否为“M类数列”?若是,指出它对应的实常数
是否为“M类数列”?若是,指出它对应的实常数 ,若不是,请说明理由;
,若不是,请说明理由;
(2)证明:若数列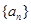 是“M类数列”,则数列
是“M类数列”,则数列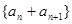 也是“M类数列”;
也是“M类数列”;
(3)若数列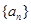 满足
满足 ,
, ,
, 为常数.求数列
为常数.求数列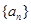 前
前 项的和.
项的和.
查看习题详情和答案>>
若数列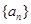 满足
满足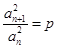 (
(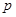 为正常数,
为正常数, ),则称
),则称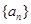 为“等方比数列”.
为“等方比数列”.
甲:数列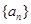 是等方比数列; 乙:数列
是等方比数列; 乙:数列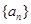 是等比数列,则( )
是等比数列,则( )
| A.甲是乙的充分条件但不是必要条件 |
| B.甲是乙的必要条件但不是充分条件 |
| C.甲是乙的充要条件 |
| D.甲既不是乙的充分条件也不是乙的必要条件 |