摘要:8. 在数列.是各项均为正数的等比数列.设. (Ⅰ)数列是否为等比数列?证明你的结论, (Ⅱ)设数列.的前项和分别为..若..求数列的前项和. 解:(Ⅰ)是等比数列.························································································· 2分 证明:设的公比为.的公比为.则 .故为等比数列.············································ 5分 (Ⅱ)数列和分别是公差为和的等差数列. 由条件得.即 .····················································································· 7分 故对..-. . 于是 将代入得...································································· 10分 从而有. 所以数列的前项和为 .······················································································ 12分
网址:http://m.1010jiajiao.com/timu3_id_528017[举报]
 ,
, 是各项均为正数的等比数列,设
是各项均为正数的等比数列,设 .(Ⅰ)数列
.(Ⅰ)数列 是否为等比数列?证明你的结论;(Ⅱ)设数列
是否为等比数列?证明你的结论;(Ⅱ)设数列 ,
, 的前
的前 项和分别为
项和分别为 ,
, .若
.若 ,
, ,求数列
,求数列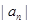 ,
,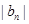 是各项均为正数的等比数列,设
是各项均为正数的等比数列,设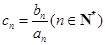 .(Ⅰ)数列
.(Ⅰ)数列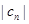 是否为等比数列?证明你的结论;(Ⅱ)设数列
是否为等比数列?证明你的结论;(Ⅱ)设数列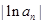 ,
,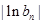 的前
的前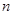 项和分别为
项和分别为 ,
,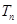 .若
.若 ,
,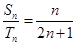 ,求数列
,求数列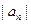 ,
,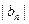 是各项均为正数的等比数列,设
是各项均为正数的等比数列,设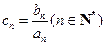 .(Ⅰ)数列
.(Ⅰ)数列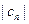 是否为等比数列?证明你的结论;(Ⅱ)设数列
是否为等比数列?证明你的结论;(Ⅱ)设数列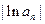 ,
,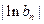 的前
的前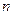 项和分别为
项和分别为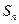 ,
,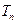 .若
.若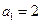 ,
,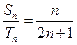 ,求数列
,求数列